题目内容
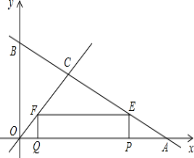
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,2),点C为线段AB上任意一点(不与点A、B重合).CD⊥OA于点D,点E在DC的延长线上,EF⊥y轴于点F,若点C为DE中点,则四边形ODEF的周长为_____.
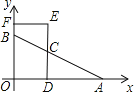
【答案】8
【解析】
首先利用待定系数法求出直线AB的解析式,由点C在直线AB上设出点C的坐标为(m,-![]() m+2),再由点C为线段DE的中点可找出点E的坐标,从而找出线段OD、DE的长度,利用ED⊥OA,EF⊥y轴,BO⊥OA可得出∠O=∠F=∠ODE=90°,从而得出四边形ODEF为矩形,再根据矩形的周长公式即可得出结论.
m+2),再由点C为线段DE的中点可找出点E的坐标,从而找出线段OD、DE的长度,利用ED⊥OA,EF⊥y轴,BO⊥OA可得出∠O=∠F=∠ODE=90°,从而得出四边形ODEF为矩形,再根据矩形的周长公式即可得出结论.
解:设直线AB的解析式为y=kx+b,
将点A(4,0)、点B(0,2)代入y=kx+b中,
得:![]() ,
,
解得: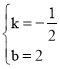 .
.
∴直线AB的解析式为y=﹣![]() x+2.
x+2.
设点C的坐标为(m,﹣![]() m+2)(0<m<4),则点E的坐标为(m,﹣m+4),
m+2)(0<m<4),则点E的坐标为(m,﹣m+4),
∴OD=EF=m,CD=2﹣![]() m,DE=4﹣m,
m,DE=4﹣m,
∵ED⊥OA,EF⊥y轴,BO⊥OA,
∴∠O=∠F=∠ODE=90°,
∴四边形ODEF为矩形.
∴C矩形ODEF=2×(OD+DE)=2×(m+4﹣m)=8.
故答案为:8.

练习册系列答案
相关题目