Question

【题目】已知抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2﹣10x+16=0的两个根，且抛物线的对称轴是直线x=﹣2．

（1）求A、B、C三点的坐标；

（2）求此抛物线的表达式；

（3）连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

（4）在（3）的基础上试说明S是否存在最大值？若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．

Answer 1

【答案】（1）A的坐标为（﹣6，0），点B的坐标为（2，0），点C的坐标为（0，8）；（2）y=﹣x2﹣x+8；（3）S=﹣m2+4m，自变量m的取值范围是0＜m＜8 ；（4）点E的坐标为（﹣2，0），△BCE为等腰三角形．

【解析】试题分析：（1）解方程x2﹣10x+16=0得x1=2，x2=8 ；根据点B、C的位置则可得B、C的坐标，再根据抛物线的对称性则可得点A的坐标；

（2）根据（1）中得到的点A、B、C的坐标，利用待定系数法即可求得抛物线的解析式；

（3）先表示出BE的长度并求出△ABC的面积，再判定△BEF和△ABC相似，然后根据相似三角形面积的比等于相似比的平方表示出△BEF的面积，再根据等高的三角形的面积的比等于底边的比列式求解即可得到S与m的关系式；

（4）根据（3）中求得的S与m的关系式，利用二次函数的性质即可求得最大值，从而确定出m值，即可对△BCE的形状作出判断.

试题解析：（1）解方程x2﹣10x+16=0得x1=2，x2=8 ；

∵点B在x轴的正半轴上，点C在y轴的正半轴上，且OB＜OC，

∴点B的坐标为（2，0），点C的坐标为（0，8）；

又∵抛物线y=ax2+bx+c的对称轴是直线x=﹣2，

∴由抛物线的对称性可得点A的坐标为（﹣6，0）；

（2）∵点C（0，8）在抛物线y=ax2+bx+c的图象上，

∴c=8，将A（﹣6，0）、B（2，0）代入表达式，

得： ，解得 ，

∴所求抛物线的表达式为y=；

（3）依题意，AE=m，则BE=8﹣m，

∵OA=6，OC=8，

∴AC=10，

∵EF∥AC，

∴△BEF∽△BAC，

∴ ，即，

∴EF= ，

过点F作FG⊥AB，垂足为G，

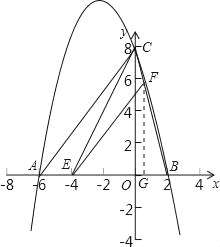
则sin∠FEG=sin∠CAB=，

∴ ,

∴FG= ，

∴S=S△BCE﹣S△BFE=（8﹣m）×8﹣（8﹣m）（8﹣m）=﹣m2+4m，

自变量m的取值范围是0＜m＜8 ；

（4）存在．

理由：∵S=﹣m2+4m=﹣（m﹣4）2+8且﹣＜0，

∴当m=4时，S有最大值，S最大值=8 ，

∵m=4，

∴点E的坐标为（﹣2，0），

∴△BCE为等腰三角形．