题目内容
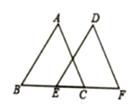
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为边
为边![]() 上一点,
上一点,![]() 为边
为边![]() 的中点,过点
的中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连结
,连结![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若点![]() 为边
为边![]() 的中点,当线段BC与线段AC满足什么数量关系时,四边形
的中点,当线段BC与线段AC满足什么数量关系时,四边形![]() 为正方形.
为正方形.

【答案】(1)证明见解析,(2)![]() 证明见解析,
证明见解析,
【解析】
(1)根据平行线的性质得到∠AFE=∠BDE,根据全等三角形的性质得到AF=BD,于是得到结论;
(2)首先证明四边形ACDF是矩形,再利用添加的条件:![]() 证明CA=CD即可解决问题;
证明CA=CD即可解决问题;
(1)证明:∵AF∥BC,
∴∠AFE=∠BDE,
![]() 为
为![]() 的中点,
的中点,
![]()
在△AEF与△BED中,

∴△AEF≌△BED,
∴AF=BD,
∵AF∥BD,
∴四边形ADBF是平行四边形;

(2)![]() 理由如下:
理由如下:
![]() 为
为![]() 的中点,
的中点,
![]() CD=DB,
CD=DB,
![]() AE=BE,
AE=BE,
∴DE∥AC,
![]()
∴∠FDB=∠C=90°,
∵AF∥BC,
∴∠AFD=∠FDB=90°,
∴∠C=∠CDF=∠AFD=90°,
∴四边形ACDF是矩形,
∵BC=2AC,CD=BD,
∴CA=CD,
∴四边形ACDF是正方形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目