题目内容
【题目】(1)(发现)如图1,在![]() 中,
中,![]() 分别交
分别交![]() 于
于![]() ,交
,交![]() 于
于![]() .已知
.已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
思考发现,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,构造
,构造![]() ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).

请回答:![]() 的值为______.
的值为______.
(2)(应用)如图3,在四边形![]() 中,
中,![]() ,
,![]() 与
与![]() 不平行且
不平行且![]() ,对角线
,对角线![]() ,垂足为
,垂足为![]() .若
.若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
(3)(拓展)如图4,已知平行四边形![]() 和矩形
和矩形![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() ,
,![]() ,判断
,判断![]() 与
与![]() 的数量关系并证明.
的数量关系并证明.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由DE//BC,EF//DC,可证得四边形DCFE是平行四边形,求出DE=CF,DC=EF,由DC⊥BE,可得△BEF是直角三角形,利用勾股定理,求出BF的长即为BC+DE的值;
(2)同(1)做CE//DB,交AB延长线于点E,易证四边形DBEC是平行四边形,根据已知可证△DAB![]() △CBA(SAS),得AC=DB,等量代换,可得AC=CE,故△ACE是等腰直角三角形,AE=8,利用勾股定理,即可求得AC;
△CBA(SAS),得AC=DB,等量代换,可得AC=CE,故△ACE是等腰直角三角形,AE=8,利用勾股定理,即可求得AC;
(3)连接AE、CE,由四边形ABCD是平行四边形,四边形ABEF是矩形,易证得四边形DCEF是平行四边形,继而证得△ACE是等腰直角三角形,求出AC=![]() CE,而DF=CE,即可得出答案.
CE,而DF=CE,即可得出答案.
解:(1)∵DE//BC,EF//DC,
∴四边形DCFE是平行四边形,
∴DE=CF,DC=EF,
∴BC+ED=BC+CF=BF,
∵DC⊥BE,DC//EF,
∴∠BEF=90°,在Rt△BEF中,
∵BE=5,EF=DC=3,
∴BF=![]() =
=![]() .
.
故BC+DE=![]() .
.
(2)做CE//DB,交AB延长线于点E,

由(1)同理,可证得四边形DBEC是平行四边形,BE=DC=3,
在△DAB和△CBA中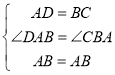 ,
,
∴△DAB![]() △CBA(SAS),
△CBA(SAS),
∴DB=AC,
∵四边形DBEC是平行四边形,DB=CE,
∴AC=CE,
∵AC⊥DB,
∴AC⊥CE,
∴△ACE是等腰直角三角形,
∵AE=AB+BE=AB+DC=5+3=8,
∴AC=![]() ,求得AC=
,求得AC=![]() .
.
故AC的长为![]() .
.
(3)AC=![]() DF;
DF;
证明:连接AE、CE,如图,
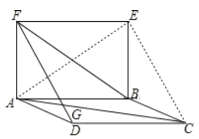
∵四边形ABCD是平行四边形,
∴AB//DC,
∵四边形ABEF是矩形,
∴AB//FE,BF=AE,
∴DC//FE,
∴四边形DCEF为平行四边形,
∴CE=DF,
∵四边形ABEF是矩形,
∴BF=AE,
∵BF=DF,
∴DF=CE,
∴AF=BE,
∵四边形ABCD是平行四边形,
∴AD=BC,
在△FAD和△EBC中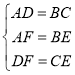 ,
,
∴△FAD![]() △EBC(SSS),
△EBC(SSS),
∴∠AFD=∠BEC,
∴∠FEB=∠EFA=90°,
∵∠EBF=60°,∠BFD=30°,
∴∠DFA=90°-30°-(90°-60°)=30°,
∴∠CEB=30°,
∴OE=OB,
∵∠EBF=60°,
∴∠BEA=∠EBF=60°,
∴∠AEC=60°+30°=90°,
即△AEC是等腰直角三角形,
∴AC=![]() CE,
CE,
∵DF=CE,
∴AC=![]() DF.
DF.
故AC与DF之间的数量关系是AC=![]() DF.
DF.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案








