题目内容
已知关于x的二次函数y=x2﹣2mx+m2+m的图象与关于x的函数y=kx+1的图象交于两点A(x1,y1)、B(x2,y2);(x1<x2)
(1)当k=1,m=0,1时,求AB的长;
(2)当k=1,m为任何值时,猜想AB的长是否不变?并证明你的猜想.
(3)当m=0,无论k为何值时,猜想△AOB的形状.证明你的猜想.
(平面内两点间的距离公式 ).
).
(1)当k=1,m=0,1时,求AB的长;
(2)当k=1,m为任何值时,猜想AB的长是否不变?并证明你的猜想.
(3)当m=0,无论k为何值时,猜想△AOB的形状.证明你的猜想.
(平面内两点间的距离公式
 ).
).(1)AB=
(2)猜想:当k=1,m为任何值时,AB的长不变,即AB= 。理由见解析。
。理由见解析。
(3)当m=0,k为任意常数时,△AOB为直角三角形,理由见解析。

(2)猜想:当k=1,m为任何值时,AB的长不变,即AB=
 。理由见解析。
。理由见解析。(3)当m=0,k为任意常数时,△AOB为直角三角形,理由见解析。
分析:(1)先将k=1,m=0分别代入,得出二次函数的解析式为y=x2,直线的解析式为y=x+1,联立
 ,得x2﹣x﹣1=0,根据一元二次方程根与系数的关系得到x1+x2=1,x1•x2=﹣1,过点A、B分别作x轴、y轴的平行线,两线交于点C,证明△ABC是等腰直角三角形,根据勾股定理得出
,得x2﹣x﹣1=0,根据一元二次方程根与系数的关系得到x1+x2=1,x1•x2=﹣1,过点A、B分别作x轴、y轴的平行线,两线交于点C,证明△ABC是等腰直角三角形,根据勾股定理得出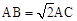 ,根据两点间距离公式及完全平方公式求出AB=
,根据两点间距离公式及完全平方公式求出AB= ;同理,当k=1,m=1时,AB=
;同理,当k=1,m=1时,AB= 。
。(2)当k=1,m为任何值时,联立
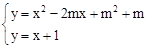 ,得x2﹣(2m+1)x+m2+m﹣1=0,根据一元二次方程根与系数的关系得到x1+x2=2m+1,x1•x2=m2+m﹣1,同(1)可求出AB=
,得x2﹣(2m+1)x+m2+m﹣1=0,根据一元二次方程根与系数的关系得到x1+x2=2m+1,x1•x2=m2+m﹣1,同(1)可求出AB= ;
;(3)当m=0,k为任意常数时,联立
 ,得x2﹣kx﹣1=0,根据一元二次方程根与系数的关系得到x1+x2=k,x1•x2=﹣1,根据两点间距离公式及完全平方公式求出AB2=k4+5k2+4,OA2+OB2═k4+5k2+4,由勾股定理的逆定理判定△AOB为直角三角形。
,得x2﹣kx﹣1=0,根据一元二次方程根与系数的关系得到x1+x2=k,x1•x2=﹣1,根据两点间距离公式及完全平方公式求出AB2=k4+5k2+4,OA2+OB2═k4+5k2+4,由勾股定理的逆定理判定△AOB为直角三角形。解:(1)当k=1,m=0时,如图,
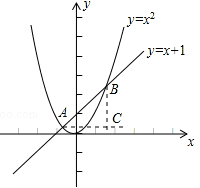
由
 得x2﹣x﹣1=0,
得x2﹣x﹣1=0,∴x1+x2=1,x1•x2=﹣1,
过点A、B分别作x轴、y轴的平行线,两线交于点C,
∵直线AB的解析式为y=x+1,
∴∠BAC=45°,△ABC是等腰直角三角形。
∴
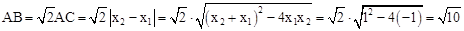 。
。同理,当k=1,m=1时,AB=
 。
。(2)猜想:当k=1,m为任何值时,AB的长不变,即AB=
 。理由如下:
。理由如下:由
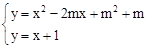 ,得x2﹣(2m+1)x+m2+m﹣1=0,
,得x2﹣(2m+1)x+m2+m﹣1=0,∴x1+x2=2m+1,x1•x2=m2+m﹣1。
∴
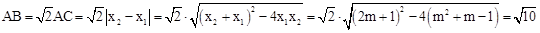 。
。(3)当m=0,k为任意常数时,△AOB为直角三角形,理由如下:
由
 ,得x2﹣kx﹣1=0,
,得x2﹣kx﹣1=0,∴x1+x2=k,x1•x2=﹣1。
∴AB2=(x1﹣x2)2+(y1﹣y2)2=(x1﹣x2)2+(kx1﹣kx2)2=(1+k2)(x1﹣x2)2
=(1+k2)[(x1+x2)2﹣4x1•x2]=(1+k2)(4+k2)=k4+5k2+4。
又∵OA2+OB2=x12+y12+x22+y22=x12+x22+y12+y22=x12+x22+(kx1+1)2+(kx2+1)2
=x12+x22+(k2x12+2kx1+1)+(k2x22+2kx2+1)=(1+k2)(x12+x22)+2k(x1+x2)+2
=(1+k2)(k2+2)+2k•k+2=k4+5k2+4,
∴AB2=OA2+OB2。
∴△AOB为直角三角形。

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

 时,y的值.
时,y的值.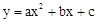 (a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
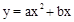 。
。 。
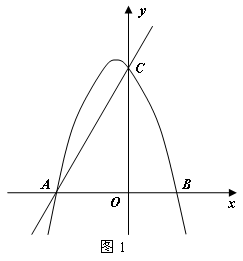
。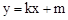 与x轴、y轴分别交于A、C两点,抛物线
与x轴、y轴分别交于A、C两点,抛物线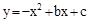 经过A、C两点,点B是抛物线与x轴的另一个交点,当
经过A、C两点,点B是抛物线与x轴的另一个交点,当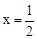 时,y取最大值
时,y取最大值 .
.
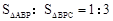 ,求点P的坐标;
,求点P的坐标; 与(1)中所求的抛物线交于M、N两点,问:
与(1)中所求的抛物线交于M、N两点,问: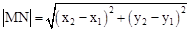 )
)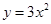 向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .
向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .