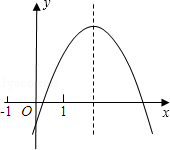题目内容
已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.
(1)求抛物线的解析式;
(2)在给出的坐标系中画出抛物线y1=ax2+bx+c(a≠0)及直线y2=x+1的图象,并根据图象,直接写出使得y1≥y2的x的取值范围;
(3)设抛物线与x轴的右边交点为A,过点A作x轴的垂线,交直线y2=x+1于点B,点P在抛物线上,当S△PAB≤6时,求点P的横坐标x的取值范围.
(1)求抛物线的解析式;
(2)在给出的坐标系中画出抛物线y1=ax2+bx+c(a≠0)及直线y2=x+1的图象,并根据图象,直接写出使得y1≥y2的x的取值范围;
(3)设抛物线与x轴的右边交点为A,过点A作x轴的垂线,交直线y2=x+1于点B,点P在抛物线上,当S△PAB≤6时,求点P的横坐标x的取值范围.
解:(1)∵抛物线与直线y2=x+1的一个交点的横坐标为2,
∴交点的纵坐标为2+1=3,即交点坐标为(2,3)。
设抛物线的解析式为y1=a(x﹣1)2+4,把交点坐标(2,3)代入得:
3=a(2﹣1)2+4,解得a=﹣1。
∴抛物线解析式为:y1=﹣(x﹣1)2+4=﹣x2+2x+3。.
(2)令y1=0,即﹣x2+2x+3=0,解得x1=3,x2=﹣1,
∴抛物线与x轴交点坐标为(3,0)和(﹣1,0)。
在坐标系中画出抛物线与直线的图形,如图:

根据图象,可知使得y1≥y2的x的取值范围为﹣1≤x≤2。
(3)由(2)可知,点A坐标为(3,0)。

令x=3,则y2=x+1=3+1=4,
∴B(3,4),即AB=4。
设△PAB中,AB边上的高为h,
则h=|xP﹣xA|=|xP﹣3|。
∴S△PAB= AB•h=
AB•h= ×4×|xP﹣3|=2|xP﹣3|.
×4×|xP﹣3|=2|xP﹣3|.
∵S△PAB≤6,∴2|xP﹣3|≤6,化简得:|xP﹣3|≤3。
去掉绝对值符号,将不等式化为不等式组:
﹣3≤xP﹣3≤3,解此不等式组,得:0≤xP≤6。
∴当S△PAB≤6时,点P的横坐标x的取值范围为0≤xP≤6。
∴交点的纵坐标为2+1=3,即交点坐标为(2,3)。
设抛物线的解析式为y1=a(x﹣1)2+4,把交点坐标(2,3)代入得:
3=a(2﹣1)2+4,解得a=﹣1。
∴抛物线解析式为:y1=﹣(x﹣1)2+4=﹣x2+2x+3。.
(2)令y1=0,即﹣x2+2x+3=0,解得x1=3,x2=﹣1,
∴抛物线与x轴交点坐标为(3,0)和(﹣1,0)。
在坐标系中画出抛物线与直线的图形,如图:

根据图象,可知使得y1≥y2的x的取值范围为﹣1≤x≤2。
(3)由(2)可知,点A坐标为(3,0)。

令x=3,则y2=x+1=3+1=4,
∴B(3,4),即AB=4。
设△PAB中,AB边上的高为h,
则h=|xP﹣xA|=|xP﹣3|。
∴S△PAB=
 AB•h=
AB•h= ×4×|xP﹣3|=2|xP﹣3|.
×4×|xP﹣3|=2|xP﹣3|.∵S△PAB≤6,∴2|xP﹣3|≤6,化简得:|xP﹣3|≤3。
去掉绝对值符号,将不等式化为不等式组:
﹣3≤xP﹣3≤3,解此不等式组,得:0≤xP≤6。
∴当S△PAB≤6时,点P的横坐标x的取值范围为0≤xP≤6。
试题分析:(1)首先求出抛物线与直线的交点坐标,然后利用待定系数法求出抛物线的解析式。
(2)确定出抛物线与x轴的两个交点坐标,依题意画出函数的图象.由图象可以直观地看出使得y1≥y2的x的取值范围。
(3)首先求出点B的坐标及线段AB的长度;设△PAB中,AB边上的高为h,则由S△PAB≤6可以求出h的范围,这是一个不等式,解不等式求出xP的取值范围。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ?若存在,请直接写出d3的值;若不存在,请说明理由.
?若存在,请直接写出d3的值;若不存在,请说明理由.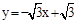 与x轴、y轴分别交于A、B两点,两动点D、E分别从A、B两点同时出发向O点运动(运动到O点停止);对称轴过点A且顶点为M的抛物线
与x轴、y轴分别交于A、B两点,两动点D、E分别从A、B两点同时出发向O点运动(运动到O点停止);对称轴过点A且顶点为M的抛物线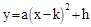 (a<0)始终经过点E,过E作EG∥OA交抛物线于点G,交AB于点F,连结DE、DF、AG、BG.设D、E的运动速度分别是1个单位长度/秒和
(a<0)始终经过点E,过E作EG∥OA交抛物线于点G,交AB于点F,连结DE、DF、AG、BG.设D、E的运动速度分别是1个单位长度/秒和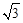 个单位长度/秒,运动时间为t秒.
个单位长度/秒,运动时间为t秒.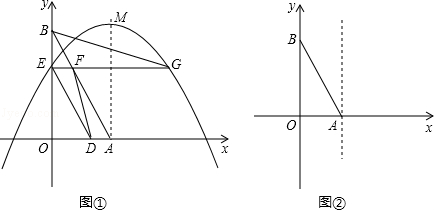
 ).
). (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表: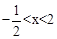 时,y<0;
时,y<0;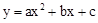 的图象如图所示,反比例函数
的图象如图所示,反比例函数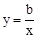 与一次函数
与一次函数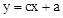 在同一平面直角坐标系中的大致图象是
在同一平面直角坐标系中的大致图象是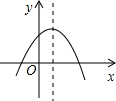
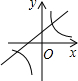
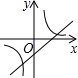
 1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:
1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论: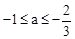 ;④3≤n≤4中,
;④3≤n≤4中,
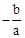 ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.