题目内容
如图,已知二次函数y=ax2+bx+c的图象经过点A(﹣4,0),B(﹣1,3),C(﹣3,3)

(1)求此二次函数的解析式;
(2)设此二次函数的对称轴为直线l,该图象上的点P(m,n)在第三象限,其关于直线l的对称点为M,点M关于y轴的对称点为N,若四边形OAPN的面积为20,求m、n的值.

(1)求此二次函数的解析式;
(2)设此二次函数的对称轴为直线l,该图象上的点P(m,n)在第三象限,其关于直线l的对称点为M,点M关于y轴的对称点为N,若四边形OAPN的面积为20,求m、n的值.
解:(1)将A(﹣4,0),B(﹣1,3),C(﹣3,3)代入y=ax2+bx+c得:
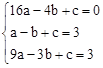 ,解得:
,解得: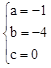 a=﹣1,b=﹣4,c=0。
a=﹣1,b=﹣4,c=0。
∴此二次函数的解析式为y=﹣4x2﹣4x。
(2)由题可知,M、N点坐标分别为(﹣4﹣m,n),(m+4,n).
∵四边形OAPF的面积=(OA+FP)÷2×|n|=20,即4|n|=20,解得|n|=5。
∵点P(m,n)在第三象限,∴n=﹣5。
∴﹣m2﹣4m+5=0,解得m=﹣5或m=1(舍去)。
∴所求m、n的值分别为﹣5,﹣5.
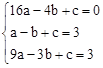 ,解得:
,解得: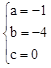 a=﹣1,b=﹣4,c=0。
a=﹣1,b=﹣4,c=0。∴此二次函数的解析式为y=﹣4x2﹣4x。
(2)由题可知,M、N点坐标分别为(﹣4﹣m,n),(m+4,n).
∵四边形OAPF的面积=(OA+FP)÷2×|n|=20,即4|n|=20,解得|n|=5。
∵点P(m,n)在第三象限,∴n=﹣5。
∴﹣m2﹣4m+5=0,解得m=﹣5或m=1(舍去)。
∴所求m、n的值分别为﹣5,﹣5.
试题分析:(1)因为抛物线y=﹣x2+bx+c过点A(﹣4,0),B(﹣1,3),C(﹣3,3)代入求出其解析式即可。
(2)由题可知,M、N点坐标分别为(﹣4﹣m,n),(m+4,n),根据四边形OAPF的面积为20,从而求出其m,n的值。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目

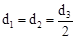 ?若存在,请直接写出d3的值;若不存在,请说明理由.
?若存在,请直接写出d3的值;若不存在,请说明理由.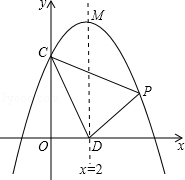
 经过点A(
经过点A( ,0)和点B(1,
,0)和点B(1, ),与x轴的另一个交点为C.
),与x轴的另一个交点为C. ∠MFO时,请直接写出线段BM的长.
∠MFO时,请直接写出线段BM的长.
 ).
).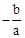 ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.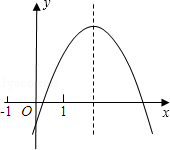
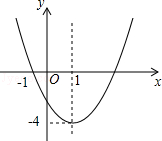

 (1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式
(1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式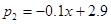 (10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;