��Ŀ����
��ͼ1��ʾ����ֱ֪��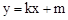 ��x�ᡢy��ֱ���A��C���㣬������
��x�ᡢy��ֱ���A��C���㣬������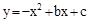 ����A��C���㣬��B����������x�����һ�����㣬��
����A��C���㣬��B����������x�����һ�����㣬��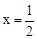 ʱ��yȡ���ֵ
ʱ��yȡ���ֵ .
.
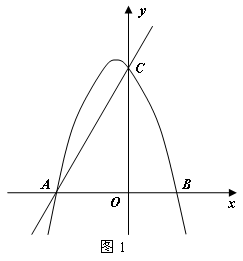
��1���������ߺ�ֱ�ߵĽ���ʽ��
��2�����P��ֱ��AC��һ�㣬��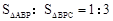 �����P�����ꣻ
�����P�����ꣻ
��3����ֱ�� �루1��������������߽���M��N���㣬��:
�루1��������������߽���M��N���㣬��:
���Ƿ����a��ֵ��ʹ�á�MON=900�������ڣ����a��ֵ���������ڣ���˵�����ɣ�
�ڲ��뵱��MON��900ʱ��a��ȡֵ��Χ����д���̣�ֱ��д���ۣ�.
���ο���ʽ����ƽ��ֱ������ϵ�У���M��x1��y1����N��x2��y2������M��N�����ľ���Ϊ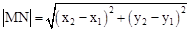 ��
��
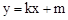 ��x�ᡢy��ֱ���A��C���㣬������
��x�ᡢy��ֱ���A��C���㣬������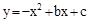 ����A��C���㣬��B����������x�����һ�����㣬��
����A��C���㣬��B����������x�����һ�����㣬��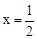 ʱ��yȡ���ֵ
ʱ��yȡ���ֵ .
.
��1���������ߺ�ֱ�ߵĽ���ʽ��
��2�����P��ֱ��AC��һ�㣬��
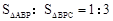 �����P�����ꣻ
�����P�����ꣻ��3����ֱ��
 �루1��������������߽���M��N���㣬��:
�루1��������������߽���M��N���㣬��:���Ƿ����a��ֵ��ʹ�á�MON=900�������ڣ����a��ֵ���������ڣ���˵�����ɣ�
�ڲ��뵱��MON��900ʱ��a��ȡֵ��Χ����д���̣�ֱ��д���ۣ�.
���ο���ʽ����ƽ��ֱ������ϵ�У���M��x1��y1����N��x2��y2������M��N�����ľ���Ϊ
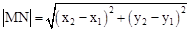 ��
����1�� ��2��
��2�� ��
�� ��3���ٴ��ڢڵ�
��3���ٴ��ڢڵ�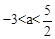 ʱ����MON��900��
ʱ����MON��900��
 ��2��
��2�� ��
�� ��3���ٴ��ڢڵ�
��3���ٴ��ڢڵ�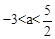 ʱ����MON��900��
ʱ����MON��900���⣺��1���ߵ�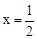 ʱ��
ʱ��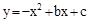 ȡ���ֵ
ȡ���ֵ ��
��
�� �����
����� ��
��
�������ߵĽ���ʽΪ ��
��
�� �����
����� ����A����3��0����B��2��0����
����A����3��0����B��2��0����
��x=0���� ����C��0��6����
����C��0��6����
��A��C���������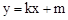 ����
����
 �����
����� ��
��
��ֱ��AC�Ľ���ʽΪ ��
��
��2�������������
�ٵ�P���߶�AC��ʱ����P��PH��x�ᣬ����ΪH��

�� ����
���� ��
��
��PH��CP�����APH�ס�ACO��
�� ����
����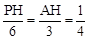 ��
��
�� ����
����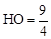 ��
��
��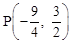 ��
��
�ڵ�P���߶�CA���ӳ�����ʱ����P��PG��x�ᣬ����ΪG��

�� ����
����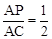 ��
��
��PG��CO�����APG�ס�ACO��
�� ����
����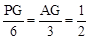 ��
��
��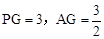 ����
���� ��
��
��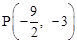 ��
��
������������P������Ϊ ��
�� ��
��
��3���ٴ��ڡ�
�������a��ֵ��ʹֱ�� �루1���������������
�루1��������������� ����M��x1��y1����N��x2��y2�����㣨M��N����ࣩ��ʹ�á�MON=900��
����M��x1��y1����N��x2��y2�����㣨M��N����ࣩ��ʹ�á�MON=900��
��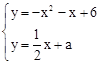 ��
��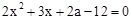 ��
��
�� ��
��
�� ��
�� ��
��
��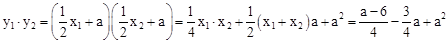 ��
��
�ߡ�MON=900���� ��
��
��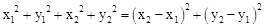 ����
���� ��
��
�� ����
���� �����
�����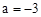 ��
��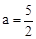 ��
��
�����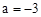 ��
��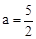 ʹ�á�MON=900��
ʹ�á�MON=900��
�ڵ�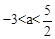 ʱ����MON��900��
ʱ����MON��900��
��1�����ݵ�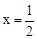 ʱ��
ʱ��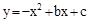 ȡ���ֵ
ȡ���ֵ ��ʽ���b��c���Ӷ��õ������ߵĽ���ʽ���������ߵĽ���ʽ�õ�A��C�����꣬�ɴ���ϵ�������ֱ��AC�Ľ���ʽ��
��ʽ���b��c���Ӷ��õ������ߵĽ���ʽ���������ߵĽ���ʽ�õ�A��C�����꣬�ɴ���ϵ�������ֱ��AC�Ľ���ʽ��
��2���ֵ�P���߶�AC�Ϻ�����������ۼ��ɡ�
��3����Ӧ��һԪ���η��̸���ϵ���Ĺ�ϵ���ɶ�����⡣
����ͼ��

��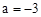 ��
��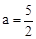 ʱ����MON=900��
ʱ����MON=900��
�� ��
�� ʱ����MON��900��
ʱ����MON��900��
��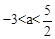 ʱ����MON��900��
ʱ����MON��900��
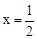 ʱ��
ʱ��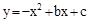 ȡ���ֵ
ȡ���ֵ ��
����
 �����
����� ��
���������ߵĽ���ʽΪ
 ��
����
 �����
����� ����A����3��0����B��2��0����
����A����3��0����B��2��0������x=0����
 ����C��0��6����
����C��0��6������A��C���������
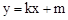 ����
���� �����
����� ��
����ֱ��AC�Ľ���ʽΪ
 ��
����2�������������
�ٵ�P���߶�AC��ʱ����P��PH��x�ᣬ����ΪH��

��
 ����
���� ��
����PH��CP�����APH�ס�ACO��
��
 ����
����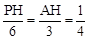 ��
����
 ����
����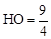 ��
����
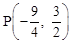 ��
���ڵ�P���߶�CA���ӳ�����ʱ����P��PG��x�ᣬ����ΪG��

��
 ����
����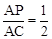 ��
����PG��CO�����APG�ס�ACO��
��
 ����
����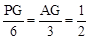 ��
����
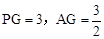 ����
���� ��
����
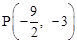 ��
��������������P������Ϊ
 ��
�� ��
����3���ٴ��ڡ�
�������a��ֵ��ʹֱ��
 �루1���������������
�루1��������������� ����M��x1��y1����N��x2��y2�����㣨M��N����ࣩ��ʹ�á�MON=900��
����M��x1��y1����N��x2��y2�����㣨M��N����ࣩ��ʹ�á�MON=900����
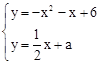 ��
��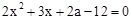 ��
����
 ��
����
 ��
�� ��
����
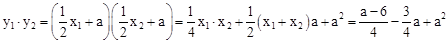 ��
���ߡ�MON=900����
 ��
����
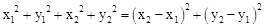 ����
���� ��
����
 ����
���� �����
�����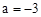 ��
��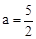 ��
�������
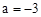 ��
��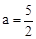 ʹ�á�MON=900��
ʹ�á�MON=900���ڵ�
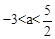 ʱ����MON��900��
ʱ����MON��900����1�����ݵ�
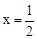 ʱ��
ʱ��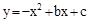 ȡ���ֵ
ȡ���ֵ ��ʽ���b��c���Ӷ��õ������ߵĽ���ʽ���������ߵĽ���ʽ�õ�A��C�����꣬�ɴ���ϵ�������ֱ��AC�Ľ���ʽ��
��ʽ���b��c���Ӷ��õ������ߵĽ���ʽ���������ߵĽ���ʽ�õ�A��C�����꣬�ɴ���ϵ�������ֱ��AC�Ľ���ʽ����2���ֵ�P���߶�AC�Ϻ�����������ۼ��ɡ�
��3����Ӧ��һԪ���η��̸���ϵ���Ĺ�ϵ���ɶ�����⡣
����ͼ��

��
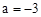 ��
��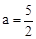 ʱ����MON=900��
ʱ����MON=900����
 ��
�� ʱ����MON��900��
ʱ����MON��900����
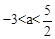 ʱ����MON��900��
ʱ����MON��900��
��ϰ��ϵ�д�
 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
�����Ŀ
 ����
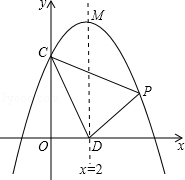
���� ������A��3��0����B����1��0����
������A��3��0����B����1��0���� ��x����������ڵ�A����y���ڵ�B����OA��OB��
��x����������ڵ�A����y���ڵ�B����OA��OB��
 ��a��0����ͼ����ͼ��ʾ�������н�������ȷ����
��a��0����ͼ����ͼ��ʾ�������н�������ȷ����
 ��a��0����һ����
��a��0����һ����
 ��1��x��9����xȡ��������10��12�µ�������p2����������·�x���㺯����ϵʽ
��1��x��9����xȡ��������10��12�µ�������p2����������·�x���㺯����ϵʽ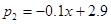 ��10��x��12����xȡ����������ȥ���ĸ������۸��������������������������
��10��x��12����xȡ����������ȥ���ĸ������۸��������������������������