题目内容
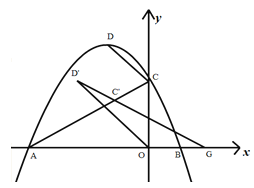
【题目】已知直线y=kx+3(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.
(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出t=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当k=![]() 时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),
时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),
①求CD的长;
②设△COD的OC边上的高为h,当t为何值时,h的值最大?


【答案】(1)①C(1,2),Q(2,0),②满足条件的t的值是1.5秒或2秒;(2)①CD=![]() ,
,
②当t为![]() 秒时,h的值最大.
秒时,h的值最大.
【解析】整体分析:
(1)①把x=1代入直线y=-x+3得到点C坐标,求出OQ的长得到点Q的坐标;②需要分两种情况讨论;(2)①过点D作DE⊥CP于点E,通过△DEC∽△AOB求CD的长;②因为CD的长和CD上的高确定,所以△OCD的面积确定,则h越大,OC就越小,当OC⊥AB时,OC最小,h最大,求出此时OP的长即可.
解:(1)①C(1,2),Q(2,0).
②由题意得:P(t,0),C(t,-t+3),Q(3-t,0).
分两种情况讨论:
情形一:当△AQC∽△AOB时,∠AQC=∠AOB=90°,∴CQ⊥OA,
∵CP⊥OA,∴点P与点Q重合,OQ=OP,
即3-t=t,∴t=1.5.
情形二:当△AQC∽△AOB时,∠ACQ=∠AOB=90°,
∵OA=OB=3,∴△AOB是等腰直角三角形,∴△ACQ也是等腰直角三角形,
∵CP⊥OA,∴AQ=2CP,即t=2(-t+3),
∴t=2.
∴满足条件的t的值是1.5秒或2秒.
(2)①由题意得:C(t,![]()
![]() )
)
∴以C为顶点的抛物线解析式是y=(x-t)2![]()
![]() ,由
,由![]() (x-t)2
(x-t)2![]()
![]() =
=![]() ,
,
解得x1=t,x2=t-![]()
![]() .
.
过点D作DE⊥CP于点E,则∠DEC=∠AOB=90°.
∵DE∥OA,∴∠EDC=∠OAB,
∴△DEC∽△AOB.
∴![]()
![]() .
.
∵AO=4,AB=5,DE=t—(t—![]() )=
)=![]() ,
,
![]() ∴CD=
∴CD=![]()
 .
.

②∵CD=![]()
![]() ,CD边上的高=
,CD边上的高=![]()
![]() ,
,
∴S△COD=![]()
![]() ,∴S△COD为定值.
,∴S△COD为定值.
要使OC边上的高h的值最大,只要OC最短,
因为当OC⊥AB时OC最短,此时OC的长为![]()
![]() ,∠BCO=90°.
,∠BCO=90°.
∵∠AOB=90°,∴∠COP=90°-∠BOC=∠OBA,
又∵CP⊥OA,
∴Rt△PCO∽Rt△OAB.
∴![]()
![]() ,OP=
,OP=
![]() ,即t=
,即t=![]() .
.![]()
∴当t为![]() 秒时,h的值最大
秒时,h的值最大![]() .
.


【题目】元旦期间,某超市对出售![]() 、
、![]() 两种商品开展元旦促销活动,活动方案有如下两种:(同一种商品不可同时参与两种活动)
两种商品开展元旦促销活动,活动方案有如下两种:(同一种商品不可同时参与两种活动)
商品 |
|
| |
标价(单位:元) |
|
| |
方案一 | 每件商品出售价格 | 按标价降价 | 按标价降价 |
方案二 | 若所购商品超过 | ||
(1)某单位购买![]() 商品
商品![]() 件,
件,![]() 商品
商品![]() 件,共花费
件,共花费![]() 元,试求
元,试求![]() 的值;
的值;
(2)在(1)求出的![]() 值的条件下,若某单位购买
值的条件下,若某单位购买![]() 商品
商品![]() 件(
件(![]() 为正整数),购买
为正整数),购买![]() 商品的件数比
商品的件数比![]() 商品件数的
商品件数的![]() 倍还多一件,请问该单位选择哪种方案才能获得最大优惠?请说明理由.
倍还多一件,请问该单位选择哪种方案才能获得最大优惠?请说明理由.
【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
收集数据
(1)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是 .
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
整理数据
(2)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 °、 °;
②估计九年级A、B类学生一共有 名.

成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
分析数据
(3)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.