题目内容
【题目】如图1,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。
与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。
(1)连接DC,求△DCE的周长;
(2)如图2,点P是线段AC上方抛物线上的一点,过P作PH⊥x 轴交x轴于点H,交线段AC于点Q,当四边形PCQC’的面积最大时,在线段PH上有一动点M,在线段DG上有一动点N,在y轴上有一动点E,且满足MN⊥PH,连接AM,MN,NE,DE,求AM+MN+NE+DE的最小值;
(3)如图3,将抛物线沿直线AC进行平移,平移过程中的点D记为D’,点C记为C’,连接D’C’所形成的直线与x轴相交于点G,请问是否存在这样的点G,使得△D’OG为等腰三角形?若存在,求出此时OG的长度,若不存在,请说明理由。


图1 图2
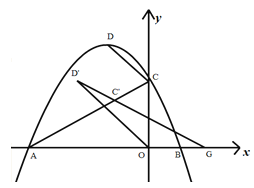
图3
【答案】(1)2![]() (2)
(2)![]() (3)OG=
(3)OG=![]() 或5或
或5或![]() 或
或![]()
【解析】分析:(1)根据函数解析式,分别求出点C,D,E的坐标,用勾股定理求CD,CE的长;(2)四边形PCQC′的面积等于PQ与CC′积的一半,CC′是的值不变,即PQ最大时,四边形PCQC′的面积最大,得到P,H的坐标,可求MN的长,分别将AM向MN方向平移MN个单位得到![]() ,过
,过![]() 轴作
轴作![]() 的对称点
的对称点![]() ,则
,则![]() +MN为所求;(3)根据D点的运动路径平行于AC,得直线DD′的解析式为
+MN为所求;(3)根据D点的运动路径平行于AC,得直线DD′的解析式为![]() ,设D′
,设D′ ,用含a的代数式表示点G的坐标,用勾股定理求OG,OD′,GD′的长,分三种情况讨论.
,用含a的代数式表示点G的坐标,用勾股定理求OG,OD′,GD′的长,分三种情况讨论.
详解:(1)可得![]() ,D(
,D(![]() )对称轴
)对称轴![]() =-1,
=-1,
∵直线AC的解析式为![]() ,∴
,∴ ,
,
∴CD= =
=![]() ;
;
CE= =
=![]() ;
;
DE=![]() .
.
∴![]() .
.
(2)设 ,
,
![]() ,
, ![]() 的值不变.
的值不变.
当PQ最大时,四边形面积最大,PQ的值最大,且![]() ,
,
当![]() 时,PQ最大,此时面积最大,
时,PQ最大,此时面积最大,  .
.
![]() ,
, ![]() ,
,
将AM向MN方向平移![]() 个单位得到
个单位得到![]() .
.
过![]() 轴作
轴作![]() 的对称点
的对称点 ,连接
,连接![]() ,交DG于点N,交y轴于点E,过N作MN∥于
,交DG于点N,交y轴于点E,过N作MN∥于![]() 轴交PH于点M,
轴交PH于点M,
此时![]() 最小,最小值=
最小,最小值=![]() .
.
(3)D点的运动路径平行于AC, 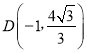 ,
,
∴![]() ,设
,设 .
.
∵∠DCA=60°,DC∥![]() .
.
∴∠C![]() G=60°,∠A
G=60°,∠A![]() G=120°.
G=120°.
∵∠CAO=30°,∴∠![]() =30°.
=30°.

∴直线D′E的解析式为y=-![]() ,∴
,∴![]() .
.
由勾股定理得:
![]() ,
,
![]() ,
,
![]() .
.
①![]() 时,
时, ![]() ,∴OG=0(舍);
,∴OG=0(舍);
②![]() 时,
时, ![]() ,∴OG=
,∴OG=![]() ;
;
③![]() 时,
时, ![]() ,∴OG=
,∴OG=![]() .
.
综上所述:OG=![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:
当温度达到设定温度﹣20℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到﹣4℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至一20℃时,制冷再次停止,..
按照以上方式循环进行
同学们记录了44min 内15个时间点冷柜中的温度y(℃) 随时间x(min) 的变化情况,制成下表:
时间x/min | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | … |
温度y/℃ | … | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | ﹣8 | ﹣12 | ﹣16 | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | a | ﹣20 | … |
(1)通过分析发现,冷柜中的温度y是时间x的函数.
①当4≤x<20时,写出一个符合表中数据的函数解析式 ;
②当20≤x<24时,写出一个符合表中数据的函数解析式 ;
(2)温度不低于﹣8℃的持续时间为 min;
(3)A的值为 .







