题目内容
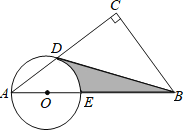
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() 交边
交边![]() 于点
于点![]() .
.

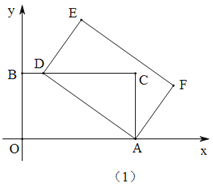
(1)当点![]() 与
与![]() 恰好重合时(如图1),求
恰好重合时(如图1),求![]() 的长;
的长;
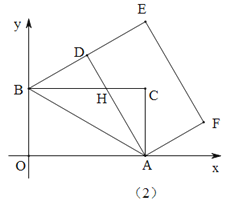
(2)问:是否可能使![]() 、
、![]() 与
与![]() 都相似?若能,请求出此时
都相似?若能,请求出此时![]() 的长;若不能,请说明理由(如图2).
的长;若不能,请说明理由(如图2).
【答案】(1)2;(2)AD =2![]() .
.
【解析】
(1)由∠DCA=∠CAB,∠ADC=∠ACB,证得△ACD∽△ABC,利用相似三角形的对应边成比例,即可求得AD的长;
(2)分别从使△ABE、△CDE与△BCE都相似分析,利用相似三角形的性质,即可求得AD的长.
解:(1)当点E与A重合时,∵CD∥AB,
∴∠DCA=∠CAB,且∠ADC=∠ACB=90°,
∴△ACD∽△ABC,
∴![]() ,
,
∴AC=2![]() ,
,
∴AD=![]() .
.
(2)若能使△ABE、△CDE与△BCE都相似,
∴∠EBC=∠A=∠D=90°,∠DEC=∠BEC=∠AEB,
∵∠DEC+∠BEC+∠AEB=180,
∴∠DEC=∠BEC=∠AEB=60°.
在Rt△DEC中,tan∠DEC=![]() ,
,
∴DE=![]() .
.
在Rt△ABE中,tan∠AEB=![]() ,
,
∴EA=![]() ,
,
∴AD=DE+AE=2![]() .
.

练习册系列答案
相关题目