Question

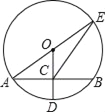
【题目】如图，圆O的半径为1，是圆O的内接等边三角形，点D.E在圆上，四边形EBCD为矩形，这个矩形的面积是_____________

Answer 1

【答案】

【解析】

连接BD、OC，根据矩形的性质得∠BCD＝90°，再根据圆周角定理得BD为⊙O的直径，则BD＝2；由ABC为等边三角形得∠A＝60°，于是利用圆周角定理得到∠BOC＝2∠A＝120°，易得∠CBD＝30°，在Rt△BCD中，根据含30°的直角三角形三边的关系得到CD＝BD＝1，BC＝CD＝，然后根据矩形的面积公式求解．

连结BD、OC，如图，

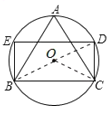
∵四边形BCDE为矩形，

∴∠BCD＝90°，

∴BD为⊙O的直径，

∴BD＝2，

∵△ABC为等边三角形，

∴∠A＝60°，

∴∠BOC＝2∠A＝120°，

而OB＝OC，

∴∠CBD＝30°，

在Rt△BCD中，CD＝BD＝1，BC＝CD＝，

∴矩形BCDE的面积＝BCCD＝

故填：．