Question

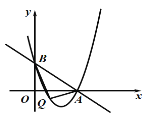
【题目】如图，在平面直角坐标系中，直线与轴、轴分别交于点、，抛物线经过、两点，且对称轴为直线.

（1）求抛物线的表达式；

（2）如果点是这抛物线上位于轴下方的一点，且△的面积是.求点的坐标.

Answer 1

【答案】（1）（2）

【解析】

（1）根据直线方程求得点A、B的坐标；然后把点A、B的坐标代入二次函数解析式，通过方程组来求系数b、c的值；
（2）如图，过Q点作QC⊥x轴并延长交直线y=-x+5于C．设点Q（m，m2-6m+5），C（m，-m+5），则QC=-m+5-（m2-6m+5）=-m2+5m．由S△ABQ=S△QCB+S△QCA得到：10＝(m2+5m)×5，则易求m的值．注意点Q位于第四象限．

解：（1）把x=0代入得，y=5；

把y=0代入得，x=5；

∴B(0，5)，A(5，0)，

将A、B两点的坐标代入，

得，

解得,

∴抛物线的解析式为;

（2）过Q点作QC⊥x轴于点D，并延长交直线于C

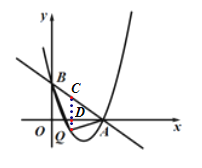
设点Q)，C(m,-m+5)，

=，

∵，

∴，

∴，

∴，

∴Q(1,0)(舍去)，Q（4，-3）.