题目内容
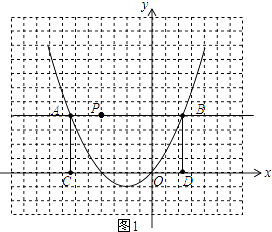
【题目】已知二次函数y=x2+x的图象,如图所示
(1)根据方程的根与函数图象之间的关系,将方程x2+x=1的根在图上近似地表示出来(描点),并观察图象,写出方程x2+x=1的根(精确到0.1).
(2)在同一直角坐标系中画出一次函数y= ![]() x+
x+ ![]() 的图象,观察图象写出自变量x取值在什么范围时,一次函数的值小于二次函数的值.
的图象,观察图象写出自变量x取值在什么范围时,一次函数的值小于二次函数的值.
(3)如图,点P是坐标平面上的一点,并在网格的格点上,请选择一种适当的平移方法,使平移后二次函数图象的顶点落在P点上,写出平移后二次函数图象的函数表达式,并判断点P是否在函数y= ![]() x+
x+ ![]() 的图象上,请说明理由.
的图象上,请说明理由.
【答案】
(1)
解:∵令y=0得:x2+x=0,解得:x1=0,x2=﹣1,
∴抛物线与x轴的交点坐标为(0,0),(﹣1,0).
作直线y=1,交抛物线与A、B两点,分别过A、B两点,作AC⊥x轴,垂足为C,BD⊥x轴,垂足为D,点C和点D的横坐标即为方程的根.
根据图形可知方程的解为x1≈﹣1.6,x2≈0.6.
(2)
解:∵将x=0代入y= ![]() x+
x+ ![]() 得y=
得y= ![]() ,将x=1代入得:y=2,
,将x=1代入得:y=2,
∴直线y= ![]() x+
x+ ![]() 经过点(0,
经过点(0, ![]() ),(1,2).
),(1,2).
直线y= ![]() x+
x+ ![]() 的图象如图所示:
的图象如图所示:
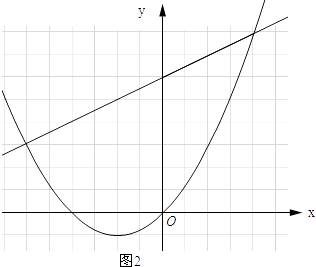
由函数图象可知:当x<﹣1.5或x>1时,一次函数的值小于二次函数的值.
(3)
解:先向上平移 ![]() 个单位,再向左平移
个单位,再向左平移 ![]() 个单位,平移后的顶点坐标为P(﹣1,1).
个单位,平移后的顶点坐标为P(﹣1,1).
平移后的表达式为y=(x+1)2+1,即y=x2+2x+2.
点P在y= ![]() x+
x+ ![]() 的函数图象上.
的函数图象上.
理由:∵把x=﹣1代入得y=1,
∴点P的坐标符合直线的解析式.
∴点P在直线y= ![]() x+
x+ ![]() 的函数图象上.
的函数图象上.
【解析】(1)令y=0求得抛物线与x的交点坐标,从而可确定出1个单位长度等于小正方形边长的4倍,接下来作直线y=1,找出直线y=1与抛物线的交点,直线与抛物线的交点的横坐标即可方程的解;(2)先求得直线上任意两点的坐标,然后画出过这两点的直线即可得到直线y= ![]() x+
x+ ![]() 的函数图象,然后找出一次函数图象位于直线下方部分x的取值范围即可;(3)先依据抛物线的顶点坐标和点P的坐标,确定出抛物线移动的方向和距离,然后依据抛物线的顶点式写出抛物线的解析式即可,将点P的坐标代入函数解析式,如果点P的坐标符合函数解析式,则点P在直线上,否则点P不在直线上.本题主要考查的是二次函数的综合应用,
的函数图象,然后找出一次函数图象位于直线下方部分x的取值范围即可;(3)先依据抛物线的顶点坐标和点P的坐标,确定出抛物线移动的方向和距离,然后依据抛物线的顶点式写出抛物线的解析式即可,将点P的坐标代入函数解析式,如果点P的坐标符合函数解析式,则点P在直线上,否则点P不在直线上.本题主要考查的是二次函数的综合应用,
解答本题主要应用坐标轴上点的坐标特点、点的坐标与函数解析式的关系,函数与方程、不等式的关系,求得抛物线与x轴的交点坐标,确定出单位长度的大小以及数形结合思想的应用是解题的关键.
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.).