题目内容
如图，函数y=-x+1与函数y=-
（x＞0）的图象交于点A，则根据图象可得不等式-x+1＜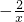
的解集是________．
x＞2
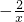分析：从图象上得到函数y=-x+1与函数y=-（x＞0）的图象交点坐标，再根据两个函数的增减性，即可得到不等式-x+1＜的解集．
解答：函数y=-x+1与函数y=-（x＞0）的图象交于点A（2，-1），
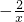当x＞2时，函数y=-（x＞0）的图象对应的点在函数y=-x+1的点的上边，不等式-x+1＜成立，
∴不等式-x+1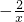＜的解集是x＞2．
故本题答案为：x＞2．
点评：本题考查了一次函数与不等式（组）的关系及数形结合思想的应用．解决此类问题关键是仔细观察图形，注意几个关键点（交点、原点等），做到数形结合．
分析：从图象上得到函数y=-x+1与函数y=-
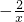（x＞0）的图象交点坐标，再根据两个函数的增减性，即可得到不等式-x+1＜的解集．解答：函数y=-x+1与函数y=-
（x＞0）的图象交于点A（2，-1），当x＞2时，函数y=-
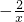（x＞0）的图象对应的点在函数y=-x+1的点的上边，不等式-x+1＜成立，∴不等式-x+1＜
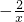的解集是x＞2．故本题答案为：x＞2．
点评：本题考查了一次函数与不等式（组）的关系及数形结合思想的应用．解决此类问题关键是仔细观察图形，注意几个关键点（交点、原点等），做到数形结合．
练习册系列答案
相关题目
如图：函数y=-kx（k≠0）与y=-
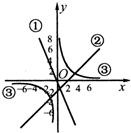如图，函数图象①、②、③的表达式应为（ ）A、y=-
| ||||
B、y=
| ||||
C、y=-
| ||||
D、y=-
|
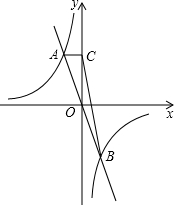如图，函数y=-kx与
如图，函数y1=k1x+b的图象与函数y2=