题目内容
【题目】已知如图△ABC中,以AB为直径的⊙O与AC,BC的交点分别为D,E.
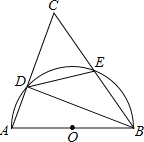
(1)∠A=68°,求∠CED的大小.
(2)当DE=BE时,证明:△ABC为等腰三角形.
【答案】(1)∠CED=68°;(2)证明见解析.
【解析】
(1)根据圆内接四边形的性质可得∠A+∠BED=180°,利用平角的定义及可得答案;
(2)由AB是直径可得∠ADB=90°,根据等腰三角形的性质可得∠EDB=∠EBD,根据角的和差关系可得∠C=∠CDE,同(1)可证明∠CDE=∠ABC,利用等量代换可得出∠C=∠ABC,即可证明△ABC为等腰三角形.
(1)∵四边形ABED为⊙O的内接四边形,
∴∠A+∠BED=180°,
∵∠BED+∠CED=180°,∠A=68°,
∴∠CED=∠A=68°.
(2)∵AB为直径,
∴∠ADB=90°,
∵ED=EB,
∴∠EDB=∠EBD,
∵∠CDE+∠EDB=90°,∠C+∠EBD=90°,
∴∠C=∠CDE,
∵四边形ABED为⊙O的内接四边形,
∴∠ADE+∠ABC=180°,
∵∠CDE+∠ADE=180°,
∴∠CDE=∠ABC,
∴∠C=∠ABC,
∴△ABC为等腰三角形.

练习册系列答案
相关题目
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数y=ax2+bx+C的最大值为6;③抛物线的对称轴是x=![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A.1个B.2个C.3个D.4个