题目内容
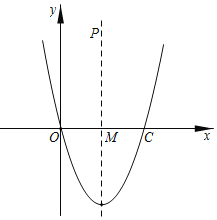
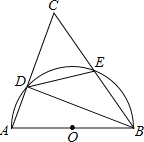
【题目】如图①,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .已知
.已知![]() 的面积是
的面积是![]() .
.
(1)求![]() 的值;
的值;
(2)在![]() 内是否存在一点
内是否存在一点![]() ,使得点
,使得点![]() 到点
到点![]() 、点
、点![]() 和点
和点![]() 的距离相等,若存在,请求出点
的距离相等,若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
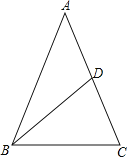
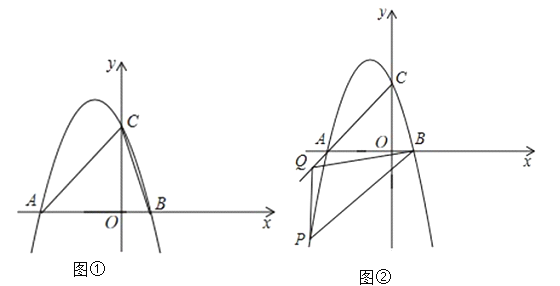
(3)如图②,![]() 是抛物线上一点,
是抛物线上一点,![]() 为射线
为射线![]() 上一点,且
上一点,且![]() 、
、![]() 两点均在第三象限内,
两点均在第三象限内,![]() 、
、![]() 是位于直线
是位于直线![]() 同侧的不同两点,若点
同侧的不同两点,若点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,
,![]() 的面积为
的面积为![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)-3;(2)存在点![]() ,使得点
,使得点![]() 到点
到点![]() 、点
、点![]() 和点
和点![]() 的距离相等;(3)
的距离相等;(3)![]() 坐标为
坐标为![]()
【解析】
(1)令![]() ,求出x的值即可求出A、B的坐标,令x=0,求出y的值即可求出点C的坐标,从而求出AB和OC,然后根据三角形的面积公式列出方程即可求出
,求出x的值即可求出A、B的坐标,令x=0,求出y的值即可求出点C的坐标,从而求出AB和OC,然后根据三角形的面积公式列出方程即可求出![]() 的值;
的值;
(2)由题意,点![]() 即为
即为![]() 外接圆圆心,即点
外接圆圆心,即点![]() 为
为![]() 三边中垂线的交点,利用A、C两点的坐标即可求出
三边中垂线的交点,利用A、C两点的坐标即可求出![]() 、
、![]() 的中点
的中点![]() 坐标,然后根据等腰三角形的性质即可得出线段
坐标,然后根据等腰三角形的性质即可得出线段![]() 的垂直平分线过原点,从而求出线段
的垂直平分线过原点,从而求出线段![]() 的垂直平分线解析式,然后求出AB中垂线的解析式,即可求出点
的垂直平分线解析式,然后求出AB中垂线的解析式,即可求出点![]() 的坐标;
的坐标;
(3)作![]() 轴交
轴交![]() 轴于
轴于![]() ,易证
,易证![]() ,从而求出
,从而求出![]() ,利用待定系数法和一次函数的性质分别求出直线AC、BP的解析式,和二次函数的解析式联立,即可求出点P的坐标,然后利用SAS证出
,利用待定系数法和一次函数的性质分别求出直线AC、BP的解析式,和二次函数的解析式联立,即可求出点P的坐标,然后利用SAS证出![]() ,从而得出
,从而得出![]() ,设
,设![]() ,利用平面直角坐标系中任意两点之间的距离公式即可求出m,从而求出点Q的坐标.
,利用平面直角坐标系中任意两点之间的距离公式即可求出m,从而求出点Q的坐标.
解:(1)![]()
令![]() ,即
,即![]()
解得![]() ,
,![]()
由图象知:![]()
![]() ,
,![]()
∴AB=1![]()
令x=0,解得y=![]()
∴点C的坐标为![]()
∴OC=![]()
![]()
![]()
解得:![]() ,
,![]() (舍去)
(舍去)
(2)存在,
由题意,点![]() 即为
即为![]() 外接圆圆心,即点
外接圆圆心,即点![]() 为
为![]() 三边中垂线的交点
三边中垂线的交点
![]() ,
,![]() ,
,
![]() ,
,![]() 、
、![]() 的中点
的中点![]() 坐标为
坐标为![]()
![]() 线段
线段![]() 的垂直平分线过原点,
的垂直平分线过原点,
设线段![]() 的垂直平分线解析式为:
的垂直平分线解析式为:![]() ,
,
将点![]() 的坐标代入,得
的坐标代入,得
![]()
解得:![]()
∴线段![]() 的垂直平分线解析式为:
的垂直平分线解析式为:![]()
![]() 由
由![]() ,
,![]() ,
,
![]() 线段
线段![]() 的垂直平分线为
的垂直平分线为![]()
将![]() 代入
代入![]() ,
,
解得:![]()
![]() 存在点
存在点![]() ,使得点
,使得点![]() 到点
到点![]() 、点
、点![]() 和点
和点![]() 的距离相等
的距离相等
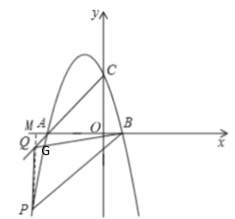
(3)作![]() 轴交
轴交![]() 轴于
轴于![]() ,则
,则![]()
∴![]()
![]() 、
、![]() 到
到![]() 的距离相等,
的距离相等,
![]()
设直线![]() ,
,
将![]() ,
,![]() 代入,得
代入,得
![]()
解得![]()
即直线![]() ,
,
∴设直线![]() 解析式为:
解析式为:![]()
![]() 直线经过点
直线经过点![]()
所以:直线![]() 的解析式为
的解析式为![]()
联立 ,
,
解得:![]()
![]() 点
点![]() 坐标为
坐标为![]()
又![]() ,
,
![]() ,
,
设AP与QB交于点G
∴GA=GQ,GP=GB
![]() ,
,
在![]() 与
与![]() 中
中
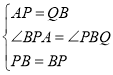 ,
,
![]()
![]() ,
,
![]()
设![]()
由![]() 得:
得:
![]()
解得:![]() ,
,![]() (当
(当![]() 时,
时,![]() ,故应舍去)
,故应舍去)
![]() 坐标为
坐标为![]() .
.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案