题目内容
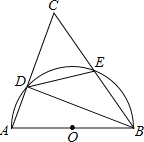
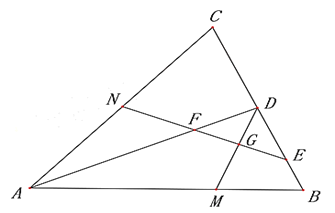
【题目】如图,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点,取EF中点G,连接DG并延长交AB于点M,延长EF交AC于点N。
(1)求证:∠FAB和∠B互余;
(2)若N为AC的中点,DE=2BE,MB=3,求AM的长.
【答案】(1)见解析;(2)AM=7
【解析】
(1)根据等腰三角形三线合一可证得AD⊥BC,根据直角三角形两锐角互余可证得结论;
(2)根据直角三角形斜边上的中线等于斜边的一半可得DG=GE即可得∠GDE=∠GED,证明△DBM∽△ECN,根据相似三角形的性质即可求得NC,继而可求AM.
解:(1) ∵AB=AC,AD为∠BAC的角平分线,
∴AD⊥BC,
∴∠FAB+∠B=90°.
(2)∵AB=AC,AD是△ABC的角平分线,
∴BD=CD,
∵DE=2BE,
∴BD=CD=3BE,
∴CE=CD+DE=5BE,
∵∠EDF=90°,点G是EF的中点,
∴DG=GE,
∴∠GDE=∠GED,
∵AB=AC,
∴∠B=∠C,
∴△DBM∽△ECN,
![]()
∵MB=3,
∴NC=5,
∵N为AC的中点,
∴AC=2CN=10,
∴AB=AC=10,
∴AM=AB-MB=7.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目