ЬтФПФкШн
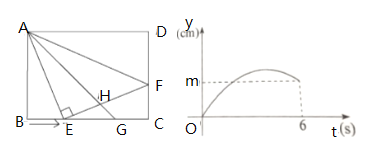
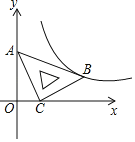
ЁОЬтФПЁПгУвЛИіДѓаЁаЮзДЙЬЖЈЕФВЛЕШБпШёНЧШ§НЧаЮжНЃЌМєГівЛИізюДѓЕФе§ЗНаЮжНБИгУЃЎМзЭЌбЇЫЕЃКЁАЕБе§ЗНаЮЕФвЛБпдкзюГЄБпЪБЃЌМєГіЕФФкНге§ЗНаЮзюДѓЁБЃЛввЭЌбЇЫЕЃКЁАЕБе§ЗНаЮЕФвЛБпдкзюЖЬБпЩЯЪБЃЌМєГіЕФФкНге§ЗНаЮзюДѓЁБЃЛБћЭЌбЇЫЕЃКЁАВЛШЗЖЈЃЌМєВЛГіетбљЕФе§ЗНаЮжНЃЎЁБФуШЯЮЊЫЫЕЕФгаЕРРэЃЌЧыжЄУїЃЎЃЈМйЩшЭМжаЁїABCЕФШ§БпaЃЌbЃЌcЃЌЧвaЃОbЃОcЃЌШ§БпЩЯЕФИпЗжБ№МЧЮЊhaЃЌhbЃЌhcЃЉ
ЁОД№АИЁПввЭЌбЇЫЕЕФе§ШЗЃЌМћНтЮі
ЁОНтЮіЁП
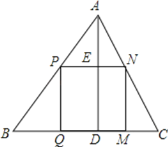
ЩшЁїABCЕФШ§ЬѕБпЩЯЕФЖдгІИпЗжБ№ЮЊhaЃЌhbЃЌhcЃЌвЛБпЗжБ№ТфдкaЃЌbЃЌcЩЯЕФФкНге§ЗНаЮБпГЄЗжБ№МЧЮЊxaЃЌxbЃЌxcЃЌРћгУЯрЫЦШ§НЧаЮаджЪПЩЕУ![]() ЃЌНјЖјБэЪОГіxaЃН
ЃЌНјЖјБэЪОГіxaЃН![]() ЃЌЭЌРэxbЃН
ЃЌЭЌРэxbЃН![]() ЃЌxcЃН
ЃЌxcЃН![]() ЃЌШЛКѓНЋЫќУЧзїВюЃЌгы0БШНЯЃЌНјЖјЕУГіxaЃЌxbЃЌxcЃЌЕФДѓаЁЙиЯЕЃЎ
ЃЌШЛКѓНЋЫќУЧзїВюЃЌгы0БШНЯЃЌНјЖјЕУГіxaЃЌxbЃЌxcЃЌЕФДѓаЁЙиЯЕЃЎ
ЩшЁїABCЕФШ§ЬѕБпЩЯЕФЖдгІИпЗжБ№ЮЊhaЃЌhbЃЌhcЃЌвЛБпЗжБ№ТфдкaЃЌbЃЌcЩЯЕФФкНге§ЗНаЮБпГЄЗжБ№МЧЮЊxaЃЌxbЃЌxcЃЌ
взЕУЃКЁїAPN~ЁїABCЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрxaЃН![]() ЃЌ
ЃЌ
ЭЌРэxbЃН![]() ЃЌxcЃН
ЃЌxcЃН![]() ЃЌ
ЃЌ
гжЩшШ§НЧаЮABCУцЛ§ЮЊs
ЁрxaЉxbЃН![]()
=![]()
=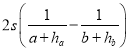
=![]() (
(![]()
=![]() )
)
ЁпaЃОbЃЌhaЃМbЃЌ
ЁрЃЈbЉaЃЉЃЈ1Љ![]() ЃЉЃМ0ЃЌ
ЃЉЃМ0ЃЌ
МДxaЉxbЃМ0ЃЌ
ЁрxaЃМxbЃЌ
ЭЌРэЃКxbЃМxcЃЌ
ЁрxaЃМxbЃМxcЃЎ
ЁрввЭЌбЇЫЕЕФе§ШЗЃЎ