题目内容
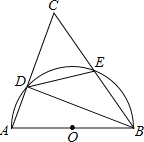
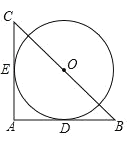
【题目】如图，已知
，
是
的中点，过点作
.求证：
与相切.
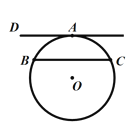
【答案】详见解析.
【解析】
证法一：连接
，
，
，
，连接
交
于点
，利用线段垂直平分线的性质和垂径定理的推论证明垂直平分，然后利用垂径定理和平行线的性质求得
，从而使问题得证；证法二：连接，，连接交于点，利用垂径定理的推论得到
，
，然后利用平行线的性质求得，从而使问题得证；证法三：过点
作
于点
，延长
交
于点
，利用垂径定理的推论得到是
的中点，然后判断点
与点是同一个点，然后然后利用平行线的性质求得，从而使问题得证.
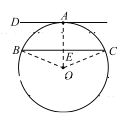
证明：证法一：连接，，，，连接交于点.
∵
，∴点在的垂直平分线上.
∵是的中点，∴
，∴
，
∴点在的垂直平分线上，
∴垂直平分，∴，
∵
，∴
，∴，
∵点为半径的外端点，
∴
与相切.
证法二：连接，，连接交于点.
∵是的中点，∴，
∴
，∴，∴，
∵，∴，∴，
∵点为半径的外端点，
∴与相切.
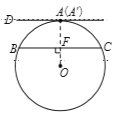
证法三：过点作于点，延长交于点，
∴
，
，∴是的中点，
∵点是的中点，∴点与点是同一个点.
∵，∴
，∴，
∵点为半径的外端点，
∴与相切.
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
相关题目
