题目内容
【题目】等腰直角三角形ABC和等腰直角三角形ADE中，∠BAC＝∠DAE＝90°，AB＝4，AE＝2，其中△ABC固定，△ADE绕点A作360°旋转，点F、M、N分别为线段BE、BC、CD的中点，连接MN、NF．
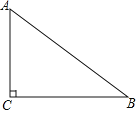
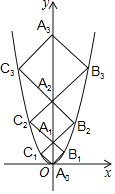
问题提出：（1）如图1，当AD在线段AC上时，则∠MNF的度数为 ，线段MN和线段NF的数量关系为 ；
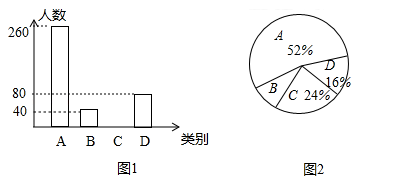
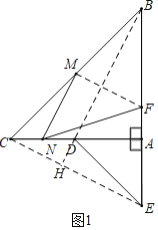
深入讨论：（2）如图2，当AD不在线段AC上时，请求出∠MNF的度数及线段MN和线段NF的数量关系；
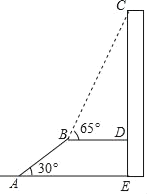
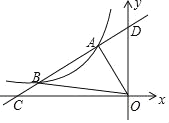
拓展延伸：（3）如图3，△ADE持续旋转过程中，若CE与BD交点为P，则△BCP面积的最小值为 ．
【答案】（1）45°，NF＝
MN；（2）∠MNF＝45°，NF＝MN；（3）4
【解析】
（1）如图1，连接DB，MF，CE，延长BD交EC于H．证明△BAD≌△CAE（SAS），推出BD＝EC，∠ACE＝∠ABD，再根据三角形中位线定理即可解决问题．
（2）如图2，连接MF，EC，BD．设EC交AB于O，BD交EC于H．证明△BAD≌△CAE（SAS），推出BD＝EC，∠ACE＝∠ABD，再利用三角形中位线定理即可解决问题．
（3）如图3中，如图3中，如图以A为圆心AD为半径作⊙A．当直线PB与⊙A相切时，△BCP的面积最小．
解：（1）如图1中，连接DB，MF，CE，延长BD交EC于H．
∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，
∴△BAD≌△CAE（SAS），
∴BD＝CE，∠ACE＝∠ABD，
∵∠ABD+∠ADB＝90°，∠ADB＝∠CDH，
∴∠CDH+∠DCH＝90°，
∴∠CHD＝90°，
∴EC⊥BH，
∵BM＝MC，BF＝FE，
∴MF∥EC，MF＝
EC，
∵CM＝MB，CN＝ND，
∴MN∥BD，MN＝BD，
∴MN＝MF，MN⊥MF，
∴∠NMF＝90°，
∴∠MNF＝45°，NF＝MN．
故答案为：45°；NF＝MN．
（2）：如图2中，连接MF，EC，BD．设EC交AB于O，BD交EC于H．
∵AC＝AB，AE＝AD，∠BAC＝∠DAE＝90°，
∴∠BAD＝∠CAE，
∴△BAD≌△CAE（SAS），
∴BD＝CE，∠ACE＝∠ABD，
∵∠AOC+∠ACO＝90°，∠AOC＝∠BOH，
∴∠OBH+∠BOH＝90°，
∴∠BHO＝90°，
∴EC⊥BD，
∵BM＝MC，BF＝FE，
∴MF∥EC，MF＝EC，
∵CM＝MB，CN＝ND，
∴MN∥BD，MN＝BD，
∴MN＝MF，MN⊥MF，
∴∠NMF＝90°，
∴∠MNF＝45°，NF＝MN．
（3）：如图3中，如图以A为圆心AD为半径作⊙A．
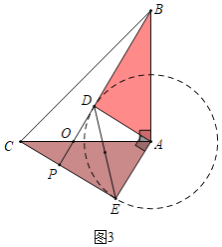
当直线PB与⊙A相切时，此时∠CBP的值最小，点P到BC的距离最小，即△BCP的面积最小，
∵AD＝AE，AB＝AC，∠BAC＝∠DAE＝90°，
∴∠BAD＝∠CAE，
∴△BAD≌△CAE（SAS），
∴∠ACE＝∠ABD，BD＝EC，
∵∠ABD+∠AOB＝90°，∠AOB＝∠CPO，
∴∠CPB＝90°，
∵PB是⊙A的切线，
∴∠ADP＝90°，
∵∠DPE＝∠ADP＝∠DAE＝90°，
∴四边形ADPE是矩形，
∵AE＝AD，
∴四边形ADPE是正方形，
∴AD＝AE＝PD＝PE＝2，BD＝EC＝
＝2
，
∴PC＝2﹣2，PB＝2+2，
∴S△BCP的最小值＝×PC×PB＝（2﹣2）（2+2）＝4．
