题目内容
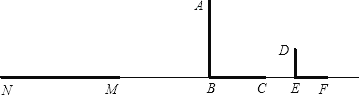
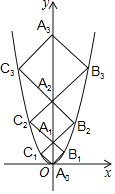
【题目】二次函数y＝x2的图象如图，点A0位于坐标原点，点A1，A2，A3…An在y轴的正半轴上，点B1，B2，B3…Bn在二次函数位于第一象限的图象上，点C1，C2，C3…n在二次函数位于第二象限的图象上，四边形A0B1A1C1，四边形A1B2A2C2，四边形A2B3A3C3…四边形An﹣1BnAnn都是正方形，则正方形An﹣1BnAnn的周长为_____．
【答案】4
n
【解析】
根据四边形A0B1A1C1是正方形，可得知△A0B1A1是等腰直角三角形，结合抛物线的解析式求出△A0B1A1的直角边长，同理求出直角△A1B2A2的直角边长……，找到直角三角形△An﹣1BnAn的直角边长的规律即可求出周长.
解：∵四边形A0B1A1C1是正方形，∠A0B1A1＝90°，
∴△A0B1A1是等腰直角三角形．
设△A0B1A1的直角边长为m1，则B1（
m，m）；
代入抛物线的解析式中得：（m）2＝m，
解得m1＝0（舍去），m1＝；
故△A0B1A1的直角边长为，
同理可求得等腰直角△A1B2A2的直角边长为2，
…
依此类推，等腰直角△An﹣1BnAn的直角边长为n，
故正方形An﹣1BnAnn的周长为4n．
故答案是：4n．
【题目】我市某校为了让学生的课余生活丰富多彩，开展了以下课外活动：
代号 | 活动类型 |
A | 经典诵读与写作 |
B | 数学兴趣与培优 |
C | 英语阅读与写作 |
D | 艺体类 |
E | 其他 |
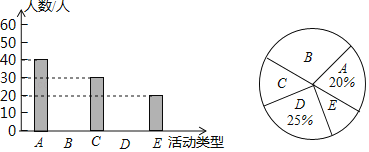
为了解学生的选择情况，现从该校随机抽取了部分学生进行问卷调查（参与问卷调查的每名学生只能选择其中一项），并根据调查得到的数据绘制了如图所示的两幅不完整的统计图．请根据统计图提供的信息回答下列问题（要求写出简要的解答过程）．
（1）此次共调查了 名学生．
（2）将条形统计图补充完整．
（3）“数学兴趣与培优”所在扇形的圆心角的度数为 ．
（4）若该校共有2000名学生，请估计该校喜欢A、B、C三类活动的学生共有多少人？
（5）学校将从喜欢“A”类活动的学生中选取4位同学（其中女生2名，男生2名）参加校园“金话筒”朗诵初赛，并最终确定两名同学参加决赛，请用列表或画树状图的方法，求出刚好一男一女参加决赛的概率．
