题目内容
【题目】已知△OBF 是直角三角形,∠BFO=90°,∠BOF=30°,△AOB 是等边三角形,OB=4,点 A 与点 F 位于直线 OB 的异侧.
(Ⅰ)如图①,求 BF 及 OF 的长;
(Ⅱ)点 P 是直线OF 上的一个动点,连接 AP,以点 A 为旋转中心,把△AOP 逆时针旋转,使边 AO 与 AB 重合,得△ABD.
①如图②,求在点 P 运动过程中,使点 D 落在线段 OF 上时 OP 的长;
②求在点 P 运动过程中,使点 P 落在线段 OF 上,且△OPD 的面积等于![]() 时 OP 的长(直接写出结果即可).
时 OP 的长(直接写出结果即可).

【答案】(1)![]() (2)①
(2)① ![]() ②
②![]()
【解析】
(I)如图①中,解直角三角形△OBF 即可;
(Ⅱ)①只要证明△PAD 是等边三角形,OA⊥PD 即可解决问题;
②如图③中,过点 B 作 BE⊥OA 于点 E,过点 D 作 DH⊥x 轴于点 H,延长 EB 交 DH 于点 G,则 BG⊥DH.根据三角形的面积公式构建方程即可解决问题;
(I)如图①中,
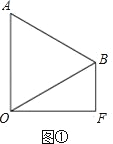
在 Rt△BOF 中,∵∠F=90°,∠BOF=30°,OB=4,
∴BF=![]() OB=2,OF=
OB=2,OF=![]() =2
=2![]() .
.
(Ⅱ)①如图②中,
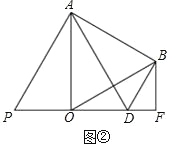
∵△AOB 是等边三角形,
∴OA=OB=AB=4,∠OAB=∠AOB=60°
由旋转可知:∠PAD=∠OAB=60°,AP=AD,
∴△APD 是等边三角形,
∵∠AOD=∠AOB+∠BOF=90°,
∴OA⊥PD,
∴OP=OD,∠PAO=∠DAO=30°,
∴OP=OAtan30°= ![]()
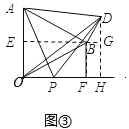 ②如图③中,过点 B 作 BE⊥OA 于点 E,过点 D 作 DH⊥x 轴于点 H,延长 EB 交 DH 于点 G,则 BG⊥DH.
②如图③中,过点 B 作 BE⊥OA 于点 E,过点 D 作 DH⊥x 轴于点 H,延长 EB 交 DH 于点 G,则 BG⊥DH.
设 BD=OP=x,
在 Rt△DBG 中,∠DBG=60°,
∴DG=BDsin60°= ![]() x.
x.
∴DH=2+ ![]() x.
x.
∵△OPD 的面积等于 ![]() ,
,
∴ ![]() x(2+
x(2+ ![]() x)=
x)=![]() ,
,
整理得:![]() x2+4x﹣
x2+4x﹣![]() =0,
=0,
解得:x= ![]() 或
或 ![]() (舍去).
(舍去).
∴OP= ![]() .
.