题目内容

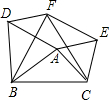
如图所示，O是矩形对角线交点，过O作EF⊥AC分别交AD，BC于E，F，若AB=2cm，BC=4cm，则四边形AECF的面积为______cm2．
先证△AOF≌△COE得到OE=OF，故四边形AECF是菱形．
设EC=x，则BE=BC-EC=4-x，
在Rt△ABE中，AE2=AB2+EB2∴x2=22+（4-x）2
解得x=
5
2

∴S菱形AECF=EC•AB=5cm2
练习册系列答案
相关题目
在四边形ABCD中，对角线AC与BD互相平分，交点为O．在不添加任何辅助线的前提下，要使四边形ABCD成为矩形，还需添加一个条件，这个条件可以是______．
将矩形ABCD沿AE折叠，得到如图所示的图形，已知∠CED′=60°，则∠AED的大小是（　　）
A．60°B．50°C．75°D．55°
如图，以△ABC的各边向同侧作正△ABD，BCF，ACE．
（1）求证：四边形AEFD是平行四边形；
（2）当△ABC是______三角形时，四边形AEFD是菱形；
（3）当∠BAC=______时，四边形AEFD是矩形；
（4）当∠BAC=______时，以A、E、F、D为顶点的四边形不存在．
（根据课本习题改编）如图1，在△ABC中，∠C=90°，AC=4，BC=3，四边形DEFG为△ABC的内接正方形，若设正方形的边长为x，容易算出x的长为
60
37
．
探究与计算：
（1）如图2，若三角形内有并排的两个全等的正方形，它们组成的矩形内接于△ABC，则正方形的边长为______；
（2）如图3，若三角形内有并排的三个全等的正方形，它们组成的矩形内接于△ABC，则正方形的边长为______；
（3）如图4，若三角形内有并排的n个全等的正方形，它们组成的矩形内接于△ABC，请你猜想正方形的边长是多少？并对你的猜想进行证明．
已知：如图，四边形ABCD是矩形（AD＞AB），点E在BC上，且AE=AD，DF⊥AE，垂足为F，
求证：DF=AB．
如图，在?ABCD中，添加一个条件可以使它成为矩形，你添加的条件是______．
如图，矩形ABCD的对角线AC、BD相交于点O，AB=1cm，∠AOB=60°，则AC=______cm，矩形ABCD的面积=______cm2．
如图，已知E是?ABCD中BC边的中点，连接AE并延长AE交DC的延长线于点F．
（1）求证：△ABE≌△FCE．
（2）连接AC、BF，若∠AEC=2∠ABC，求证：四边形ABFC为矩形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网