题目内容
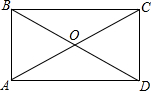
（根据课本习题改编）如图1，在△ABC中，∠C=90°，AC=4，BC=3，四边形DEFG为△ABC的内接正方形，若设正方形的边长为x，容易算出x的长为
．
探究与计算：
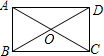
（1）如图2，若三角形内有并排的两个全等的正方形，它们组成的矩形内接于△ABC，则正方形的边长为______；
（2）如图3，若三角形内有并排的三个全等的正方形，它们组成的矩形内接于△ABC，则正方形的边长为______；
（3）如图4，若三角形内有并排的n个全等的正方形，它们组成的矩形内接于△ABC，请你猜想正方形的边长是多少？并对你的猜想进行证明．
| 60 |
| 37 |
探究与计算：
（1）如图2，若三角形内有并排的两个全等的正方形，它们组成的矩形内接于△ABC，则正方形的边长为______；
（2）如图3，若三角形内有并排的三个全等的正方形，它们组成的矩形内接于△ABC，则正方形的边长为______；
（3）如图4，若三角形内有并排的n个全等的正方形，它们组成的矩形内接于△ABC，请你猜想正方形的边长是多少？并对你的猜想进行证明．
（1）
；（2分）
（2）
；（2分）
（3）若三角形内有并排的n个全等的正方形，它们组成的矩形内接于△ABC，正方形的边长是
．（2分）
证明，如图，
过点C作CN⊥AB，垂足为N，交GF于点M，
设小正方形的边长为x，
∵四边形GDEF为矩形，∴GF∥AB，CM⊥GF，
易算出CN=
，
∴
=
，即
=
，
∴x=
．
即小正方形的边长是
．（4分）
| 60 |
| 49 |
（2）
| 60 |
| 61 |
（3）若三角形内有并排的n个全等的正方形，它们组成的矩形内接于△ABC，正方形的边长是
| 60 |
| 25+12n |
证明，如图，
过点C作CN⊥AB，垂足为N，交GF于点M，
设小正方形的边长为x，
∵四边形GDEF为矩形，∴GF∥AB，CM⊥GF，
易算出CN=
| 12 |
| 5 |
∴
| CM |
| CN |
| GF |
| AB |
| ||
|
| nx |
| 5 |
∴x=
| 60 |
| 25+12n |
即小正方形的边长是
| 60 |
| 25+12n |
练习册系列答案
相关题目
