Question

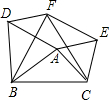
如图，以△ABC的各边向同侧作正△ABD，BCF，ACE．
（1）求证：四边形AEFD是平行四边形；
（2）当△ABC是______三角形时，四边形AEFD是菱形；
（3）当∠BAC=______时，四边形AEFD是矩形；
（4）当∠BAC=______时，以A、E、F、D为顶点的四边形不存在．

Answer 1

（1）证明：∵△BCF和△ACE是等边三角形，
∴AC=CE，BC=CF，∠ECA=∠BCF=60°，
∴∠ECA-∠FCA=∠BCF-∠FCA，
即∠ACB=∠ECF，
∵在△ACB和△ECF中

AC=CE ∠ACB=∠ECF BC=CF

，
∴△ACB≌△ECF（SAS），
∴EF=AB，
∵三角形ABD是等边三角形，
∴AB=AD，
∴EF=AD=AB，
同理FD=AE=AC，
即EF=AD，DF=AE，
∴四边形AEFD是平行四边形．

（2）当△ABC是等腰三角形时，平行四边形AEFD是菱形，理由如下：
∵由（1）知：四边形AEFD是平行四边形，EF=AD=AB，FD=AE=AC
∴AB=AC，
∴EF=FD，
∴平行四边形AEFD是菱形，
故答案为：等腰．

（3）当∠BAC=150°时，平行四边形AEFD是矩形，理由如下：
∵△ADB和△ACE是等边三角形，
∴∠DAB=∠EAC=60°，
∵∠BAC=150°，
∴∠DAE=360°-60°-60°-150°=90°，
∵由（1）知：四边形AEFD是平行四边形，
∴平行四边形AEFD是矩形，
故答案为：150°．

（4）当∠BAC=60°时，以A、E、F、D为顶点的四边形不存在，理由如下：
∵∠DAB=∠EAC=60°（已证），∠BAC=60°，
∴∠DAE=60°+60°+60°=180°，
∴D、A、E三点共线，
即边DA、AE在一条直线上，
∴当∠BAC=60°时，以A、E、F、D为顶点的四边形不存在，
故答案为：60°．