题目内容
【题目】在平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“距离”,记作![]() 特别地,若图形M,N有公共点,规定
特别地,若图形M,N有公共点,规定![]() .
.

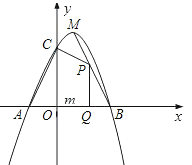
![]() 如图1,
如图1,![]() 的半径为2,
的半径为2,
![]() 点
点![]() ,
,![]() ,则
,则![]() ______,
______,![]() ______.
______.
![]() 已知直线l:
已知直线l:![]() 与
与![]() 的“距离”
的“距离”![]() ,求b的值.
,求b的值.
![]() 已知点
已知点![]() ,
,![]() ,
,![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() 若
若![]() ,请直接写出m的取值范围______.
,请直接写出m的取值范围______.
【答案】(1)![]() 1 , 3,
1 , 3,![]() ;(2)m的值为
;(2)m的值为![]() 或
或![]() 或
或![]() .
.
【解析】
![]() 根据图形M,N间的“距离”的定义即可解决问题;
根据图形M,N间的“距离”的定义即可解决问题;
![]() 设直线l交x轴,y轴于点P,Q,作
设直线l交x轴,y轴于点P,Q,作![]() 于H,OH交
于H,OH交![]() 于
于![]() 根据
根据![]() 与
与![]() 的“距离”
的“距离”![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
![]() 如图2中,设AC交x轴于
如图2中,设AC交x轴于![]() 分四种情形分别求解即可解决问题.
分四种情形分别求解即可解决问题.
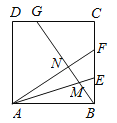
![]() 如图1中,连接OB交
如图1中,连接OB交![]() 于点E,设
于点E,设![]() 交y轴于点F.
交y轴于点F.

由题意:![]() ,
,![]() ,
,
故答案为1,3.
![]() 如图1中,设直线l交x轴,y轴于点P,Q,作
如图1中,设直线l交x轴,y轴于点P,Q,作![]() 于H,OH交
于H,OH交![]() 于G.
于G.
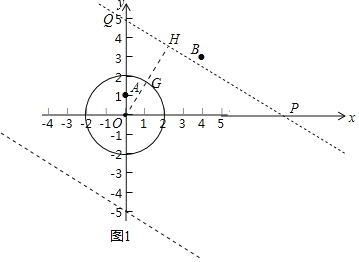
由题意:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线l:
直线l:![]() 与
与![]() 的“距离”
的“距离”![]() ,
,
![]() ,
,
![]() .
.
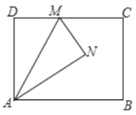
![]() 如图2中,设AC交x轴于E.
如图2中,设AC交x轴于E.
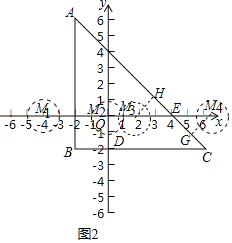
![]() ,
,
![]() 当
当![]() 时,
时,![]() 满足条件,
满足条件,
当![]() 时,
时,![]() 满足条件,
满足条件,
假设![]() 满足条件,作
满足条件,作![]() ,
,
由题意![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
观察图象可知:当![]() 时,
时,![]() 满足条件,
满足条件,
假设![]() 满足条件,作
满足条件,作![]() 于G,
于G,
由题意;![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上所述,满足条件的m的值为![]() 或
或![]() 或
或![]() .
.
故答案为4或![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】书籍是人类进步的阶梯.联合国教科文组织把每年的4月23日确定为“世界读书日”.某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:一个学期平均一天阅读课外书籍所有时间统计表
时间(分钟) | 20 | 40 | 60 | 80 | 100 | 120 |
人数(名) | 43 | 31 | 15 | 5 | 4 | 2 |
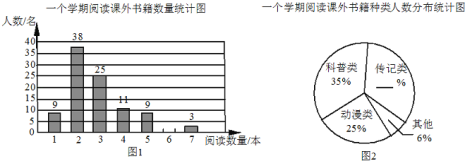
请你根据以上信息解答下列问题:
(1)补全图1、图2;
(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有4000名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?
(3)根据统计表,求一个学期平均一天阅读课外书籍所用时间的众数和中位数.