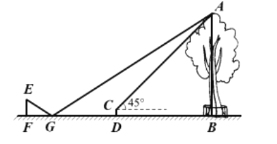
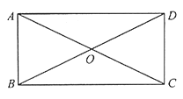
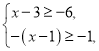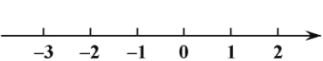题目内容
【题目】已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值:
(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
【答案】(1)k=-3;(2)点P的坐标为(2,-5)或(-2,-5).
【解析】
(1)根据抛物线的对称轴是y轴以及对称轴公式可得关于k的方程,解方程后再根据抛物线与x轴的交点个数即可确定答案;
(2)由点P到y轴的距离即可确定出点P的横坐标,再根据抛物线的解析式即可求得点P的纵坐标即可得答案.
(1)∵抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,
∴![]() ,
,
即k2+k-6=0,
解得k=-3或k=2,
当k=2时,二次函数解析式为y=x2+6,它的图象与x轴无交点,不满足题意,舍去,
当k=-3时,二次函数解析式为y=x2-9,它的图象与x轴有两个交点,满足题意,
∴k=-3;
(2)∵P到y轴的距离为2,
∴点P的横坐标为-2或2,
当x=2时,y=-5;
当x=-2时,y=-5,
∴点P的坐标为(2,-5)或(-2,-5).

【题目】甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中不超过200元的不打折,超过200元后的价格部分打7折.
设商品原价为x元,顾客购物金额为y元.
(I).根据题意,填写下表:
商品原价 | 100 | 150 | 250 | … |
甲商场购物金额(元) | 80 | … | ||
乙商场购物金额(元) | 100 | … |
(Ⅱ).分别就两家商场的让利方式写出y关于x的函数关系式;
(Ⅲ).若x≥500时,选择哪家商场去购物更省钱?并说明理由.
【题目】柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数 | 30 | 75 | 130 | 210 | 480 | 856 | 1250 | 2300 |
发芽数 | 28 | 72 | 125 | 200 | 457 | 814 | 1187 | 2185 |
发芽频率 | 0.9333 | 0.9600 | 0.9615 | 0.9524 | 0.9521 | 0.9509 | 0.9496 | 0.9500 |
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是_____(结果精确到0.01).