题目内容
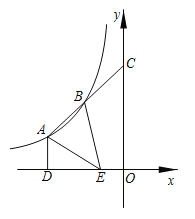
【题目】已知二次函数图象的顶点坐标为![]() ,且过点
,且过点![]() ,
,
(1)求抛物线的解析式;
(2)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)y=3(x-1)2-3;(2)当0≤x≤3时,-3≤y≤9.
【解析】
(1)已知抛物线的顶点坐标,则可设顶点式y=a(x-1)2-3,然后把点P(2,0)代入后计算出a的值即可;
(2)先根据二次函数图象的对称轴,得出当![]() 时,函数的增减性,再求出x=0与x=3时y的值,进而可得出结论.
时,函数的增减性,再求出x=0与x=3时y的值,进而可得出结论.
解:(1)设抛物线的解析式为y=a(x-1)2-3,
把点P(2,0)代入得a(2-1)2-3=0,
解得a=3,
所以抛物线的解析式为y=3(x-1)2-3;
(2)∵抛物线y=3(x-1)2-3的对称轴为x=1,
∴当0≤x≤3时,y的最小值为-3,
又当x=0时,y=0;当x=3时,y=9,
∴当0≤x≤3时,-3≤y≤9.

【题目】某科研小组计划对某一品种的西瓜用两种种植技术种植.在选择种植技术时,该科研小组主要关心的问题是:西瓜的产量和产量的稳定性,以及西瓜的优等品率.为了解这两种种植技术种出的西瓜的质量情况,科研小组各对两块自然条件相同的试验田进行对比试验,并从这两块实验田中随机抽取20个西瓜,分别称重后,将称重的结果记录如下:
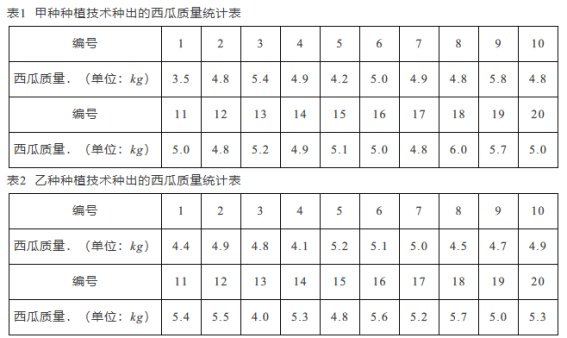
回答下列问题:
(1)若将质量为4.5~5.5(单位:kg)的西瓜记为优等品,完成下表:
优等品西瓜个数 | 平均数 | 方差 | |
甲种种植技术种出的西瓜质量 | 4.98 | 0.27 | |
乙种种植技术种出的西瓜质量 | 15 | 4.97 | 0.21 |
(2)根据以上数据,你认为该科研小组应选择哪种种植技术?并说明理由.
【题目】温州某企业安排![]() 名工人生产甲、乙两种产品,每人每天生产
名工人生产甲、乙两种产品,每人每天生产![]() 件甲或
件甲或![]() 件乙,甲产品每件可获利
件乙,甲产品每件可获利![]() 元.根据市场需求和生产经验,乙产品每天产量不少于
元.根据市场需求和生产经验,乙产品每天产量不少于![]() 件,当每天生产
件,当每天生产![]() 件时,每件可获利
件时,每件可获利![]() 元, 每增加
元, 每增加![]() 件,当天平均每件利润减少
件,当天平均每件利润减少![]() 元.设每天安排
元.设每天安排![]() 人生产乙产品.
人生产乙产品.
![]() 根据信息填表:
根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | __________ | _____________ |
|
乙 |
|
| _____________ |
![]() 若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,求每件乙产品可获得的利润.
元,求每件乙产品可获得的利润.