题目内容
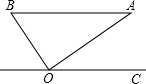
如图，已知A、B两点的坐标分别为(2
，0)、（0，2），P是△AOB外接圆上的一点，且∠AOP=45°，则点P的坐标为______．
| 3 |
∵OB=2，OA=2
，
∴AB=
=4，
∵∠AOP=45°，
P点横纵坐标相等，可设为a，
∵∠AOB=90°，
∴AB是直径，
∴Rt△AOB外接圆的圆心为AB中点，坐标C（
，1），
P点在圆上，P点到圆心的距离为圆的半径2．
过点C作CF∥OA，过点P作PE⊥OA于E交CF于F，
∴∠CFP=90°，
∴PF=a-1，CF=a-
，PC=2，
∴（a-
）2+（a-1）2=22，舍去不合适的根，
可得a=1+
，P（1+
，1+
）；
∵P与P′关于圆心（
，1）对称，
∴P′（
-1，1-
）．
故答案为：（
+1，
+1）或（
-1，1-
）
| 3 |
∴AB=
| OA2+OB2 |
∵∠AOP=45°，
P点横纵坐标相等，可设为a，
∵∠AOB=90°，
∴AB是直径，
∴Rt△AOB外接圆的圆心为AB中点，坐标C（
| 3 |
P点在圆上，P点到圆心的距离为圆的半径2．
过点C作CF∥OA，过点P作PE⊥OA于E交CF于F，
∴∠CFP=90°，
∴PF=a-1，CF=a-
| 3 |
∴（a-
| 3 |
可得a=1+
| 3 |
| 3 |
| 3 |
∵P与P′关于圆心（
| 3 |
∴P′（
| 3 |
| 3 |
故答案为：（
| 3 |
| 3 |
| 3 |
| 3 |
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
