题目内容
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,-4) ,B(3,-3) ,C(1,-1).(每个小方格都是边长为一个单位长度的正方形)
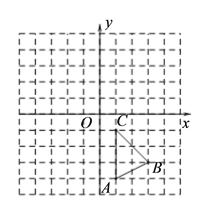
(1)将△ABC沿y轴方向向上平移5个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕点O顺时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点A旋转到点A2所经过的路径长.
【答案】(1)画图见解析;(2)画图见解析,点A旋转到点A2所经过的路径长为![]()
【解析】
(1)按题中要求在平面直角坐标系中画出点A1、B1、C1三点,再顺次连接这三点即可得到所求三角形;
(2)连接OA,在第三象限作OA2⊥OA,并使OA2=OA,即可得到点A2,同法作出点B2、C2,再顺次连接所得三点即可得到所求三角形;由题意和所在图形可知,点A旋转到A2所经过路径的长度是以点O为圆心,OA为半径,圆心角度数为90度的弧的长度,因此根据题中已知条件计算出![]() 的长度即可;
的长度即可;
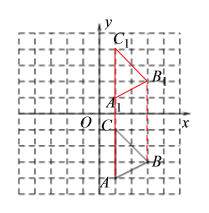
(1)如下图,△A1B1C1为所求三角形:
(2)如下图,△A2B2C2为所求三角形:
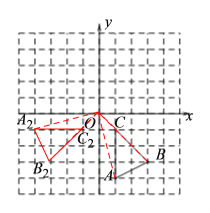
如上图,由题意可知点A旋转到点A2所经过的路径是![]() ,
,
∵OA=![]() ,∠AOA2=90°,
,∠AOA2=90°,
∴![]() .
.
∴点A旋转到点A2所经过的路径长为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目