题目内容
【题目】如图,平行四边形ABCD中,E为AB边上一点,DE=DC,点F为线段DE上一点,满足∠DFC=∠A,连结CE.
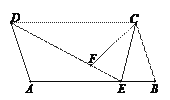
(1)求证:AD=FC;
(2)求证:CE是∠BCF的角平分线.
【答案】(1)见解析;(2)见解析
【解析】(1)由平行四边形性质,及DE=DC,∠DFC=∠A,证△ADE≌△FCD(AAS),得AD=FC.
(2)由△A DE≌△FCD得AE=FD,根据平行四边形性质,再证BE=FE, CF=CB,可再证△CEF≌△CEB(SSS).可得∠FCE=∠BC.
证明:(1)∵四边形ABCD平行四边形,
∴AB∥CD.∴∠AED=∠FDC,
又∵∠A=∠DFC,DE=CD.
∴ △ADE≌△FCD(AAS).
∴AD=FC
(2)∵△A DE≌△FCD
∴AE=FD,
∵BE=AB-AE,EF=DE-DF,
∵四边形ABCD平行四边形,
∴AB=DC,又∵DE=DC,AD=FC,
∴BE=FE, CF=CB,
又∵CE=CE.
∴ △CEF≌△CEB(SSS).
∴∠FCE=∠BCE
∴CE是∠BCF的角平分线.

练习册系列答案
相关题目
【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?