题目内容
【题目】四边形![]() 是正方形,
是正方形,![]() 是直线
是直线![]() 上任意一点,
上任意一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .当点G在BC边上时(如图1),易证DF-BE=EF.
.当点G在BC边上时(如图1),易证DF-BE=EF.

(1)当点![]() 在
在![]() 延长线上时,在图2中补全图形,写出
延长线上时,在图2中补全图形,写出![]() 、
、![]() 、
、![]() 的数量关系,并证明;
的数量关系,并证明;
(2)当点![]() 在
在![]() 延长线上时,在图3中补全图形,写出
延长线上时,在图3中补全图形,写出![]() 、
、![]() 、
、![]() 的数量关系,不用证明.
的数量关系,不用证明.
【答案】(1)图详见解析,BE=DF+EF,证明详见解析;(2)图详见解析,EF=DF+BE.
【解析】
(1)根据题意,补全图形,DF、BE、EF的数量关系是:BE=DF+EF,易证△ABE≌△DAF,根据全等三角形的性质可得AF=BE,DF=AE, 由此可得BE=AF=AE+EF=DF+EF; (2)根据题意,补全图形,DF、BE、EF的数量关系是:EF=DF+BE;易证△ABE≌△DAF,根据全等三角形的性质可得AF=BE,DF=AE, 由此可得EF=AE+AF=DF+BE.
(1)如图2,DF、BE、EF的数量关系是:BE=DF+EF,
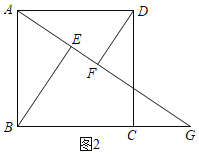
理由是:∵ABCD是正方形,
∴AB=DA,∠BAD=90°.
∵BE⊥AG,DF⊥AG,
∴∠AEB=∠AFD=90°,
又∵∠BAE+∠DAF=90°,∠BAE+∠ABE=90°,
∴∠ABE=∠DAF,
在△ABE和△DAF中,
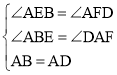 ,
,
∴△ABE≌△DAF(AAS),
∴AF=BE,DF=AE,
∴BE=AF=AE+EF=DF+EF;
(2)如图3,DF、BE、EF的数量关系是:EF=DF+BE;
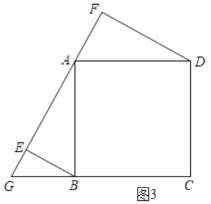
理由是:∵ABCD是正方形,
∴AB=DA,∠BAD=90°.
∵BE⊥AG,DF⊥AG,
∴∠AEB=∠AFD=90°,
又∵∠BAE+∠DAF=90°,∠BAE+∠ABE=90°,
∴∠ABE=∠DAF,
在△ABE和△DAF中,
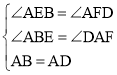 ,
,
∴△ABE≌△DAF(AAS),
∴AF=BE,DF=AE,
∴EF=AE+AF=DF+BE.

 阅读快车系列答案
阅读快车系列答案