题目内容
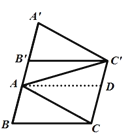
【题目】如图,将三角形ABC沿射线BA方向平移到三角形A'B'C'的位置,连接AC'.
(1)AA'与CC'的位置关系为 ;
(2)求证:∠A'+∠CAC'+∠AC'C=180°;
(3)设![]() ∠ACB=y,试探索∠CAC'与x,y之间的数量关系,并证明你的结论.
∠ACB=y,试探索∠CAC'与x,y之间的数量关系,并证明你的结论.

【答案】(1平行;(2)证明见解析;(3)∠CAC′=x+y.证明见解析.
【解析】
(1)由平移的性质直接得到答案,
(2)先证明四边形![]() 是平行四边形,利用平行四边形的性质及三角形内角和定理可得答案,
是平行四边形,利用平行四边形的性质及三角形内角和定理可得答案,
(3)过点A作AD∥![]() ,交
,交![]() 于点D,利用平行线的性质及角的和差可得答案.
于点D,利用平行线的性质及角的和差可得答案.
解:(1)由平移的性质得:![]()
故答案为:平行.
(2)证明:根据平移性质可知![]() ∥AC,
∥AC,![]() ∥
∥![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
![]()
![]()
∴∠A'+∠CAC'+∠AC'C=180°.
(3)结论:![]()
证明:过点A作AD∥![]() ,交
,交![]() 于点D.
于点D.
根据平移性质可知![]() ∥
∥![]() ,∴
,∴![]() ∥AD∥
∥AD∥![]() ,
,
∴![]()
∴![]() .
.
即![]()

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目