题目内容
【题目】如图,在四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:四边形AFCE是平行四边形.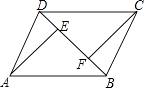
【答案】证明:连接AF、CE.

∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,AE∥CF,
∵BE=DF,
∴DE=BF,
在Rt△ADE后Rt△CBF中,
![]() ,
,
∴Rt△ADE≌Rt△CBF,
∴AE=CF,∵AE∥CF,
∴四边形AECF是平行四边形
【解析】要证四边形AECF是平行四边形,连接AF、CE.由已知AE⊥BD,CF⊥BD,可证得AE∥CF,再证明AE=CF,通过证Rt△ADE≌Rt△CBF即可。
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.





