题目内容
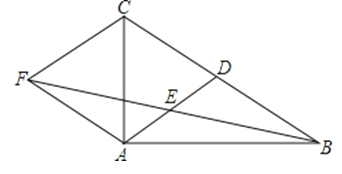
【题目】如图，在Rt△ABC中，∠B=90°，点E是AC的中点，AC=2AB，∠BAC的平分线AD交BC于点D，作AF∥BC，连接DE并延长交AF于点F，连接FC．
求证：四边形ADCF是菱形．
【答案】证明过程见解析
【解析】试题分析：先证明△AEF≌△CED，推出四边形ADCF是平行四边形，再证明∠DAC=∠ACB，推出DA=DC，由此即可证明．
试题解析：∵AF∥CD， ∴∠AFE=∠CDE，
在△AFE和△CDE中，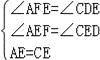
， ∴△AEF≌△CED， ∴AF=CD，∵AF∥CD，
∴四边形ADCF是平行四边形，
∵∠B=90°，∠ACB=30°， ∴∠CAB=60°， ∵AD平分∠CAB， ∴∠DAC=∠DAB=30°=∠ACD，
∴DA=DC， ∴四边形ADCF是菱形．
练习册系列答案
相关题目
