题目内容
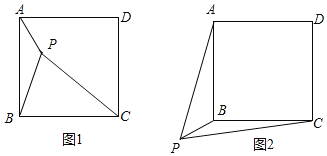
【题目】如图所示,在![]() 的方格纸中,每个小正方形的边长均为1,线段
的方格纸中,每个小正方形的边长均为1,线段![]() 的端点
的端点![]() 、
、![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
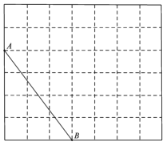
(1)在图中画出以![]() 为斜边的直角三角形
为斜边的直角三角形![]() ,点
,点![]() 在小正方形顶点上,且
在小正方形顶点上,且![]() ;
;
(2)在图中画出等腰三角形![]() ,点
,点![]() 在小正方形的顶点上,且
在小正方形的顶点上,且![]() 的面积为
的面积为![]() ;
;
(3)连接![]() ,请直接写出
,请直接写出![]() 的值.
的值.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)根据勾股定理求出AB,然后根据正切值可设BC=x,则AC=2x,然后根据勾股定理列出方程即可求出BC和AC,然后作弧即可确定点C的位置;
(2)若AB=AD=5时,利用勾股定理求出BD,然后作弧即可确定点D的位置,根据平行线之间的距离处处相等,过点D作AB的平行线,由图易知,与网格还有另外一个交点,但与A、B不能构成等腰三角形,从而确定结论;
(3)根据图形即可得出结论.
解:(1)根据勾股定理可得AB=![]()
∵![]() ,可设BC=x,则AC=2x
,可设BC=x,则AC=2x
根据勾股定理可得BC2+AC2=AB2
∴x2+(2x)2=52
解得:x=![]()
∴BC=![]() ,AC=
,AC=![]()
∵2个小正方形构成的矩形的对角线=![]() ,2个“田”字形构成的矩形的对角线=
,2个“田”字形构成的矩形的对角线=![]()
∴以B为圆心,2个小正方形构成的矩形的对角线的长为半径作弧,以A为圆心,2个“田”字形构成的矩形的对角线的长为半径作弧,两弧交于点C,连接AC、BC,如图所示,△ABC即为所求;
(2)若AB=AD=5时,如下图所示,过点D作DH⊥AB于H
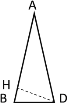
∵![]() 的面积为
的面积为![]()
∴DH=![]() ×2÷AB=
×2÷AB=![]()
根据勾股定理AH=![]()
∴BH=AB-AH=![]()
根据勾股定理BD=![]() ,而1个小正方形的对角线=
,而1个小正方形的对角线=![]()
故在网格中以A为圆心,AB的长为半径作弧,以B为圆心,以1个小正方形的对角线为半径作弧,两弧交于点D,连接AD、BD,
根据平行线之间的距离处处相等,过点D作AB的平行线,由图易知,与网格还有另外一个交点,但与A、B不能构成等腰三角形,
综上:△ABD即为所求,
(3)由图可知:CD=1,BD=![]() ,
,
∴![]() =
=![]()


【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
(1)(收集数据)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是________.
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
(2)(整理数据)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
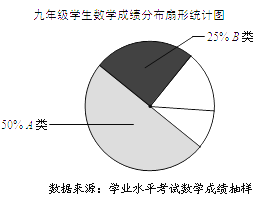
①C类和D类部分的圆心角度数分别为________°、________°;
②估计九年级A、B类学生一共有________名.
(3)(分析数据)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系,关于销售单价,日销售量,日销售利润的几组对应值如表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | 25 |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y与x的函数关系式;
(2)当销售单价x为多少元时,日销售利润w最大?最大利润是多少元?
(3)当销售单价x为多少元时,日销售利润w在1500元以上?(请直接写出x的范围)