��Ŀ����
����Ŀ����ͼ���ھ���ABCD�У�AB��4��BC��3����P�DZ�AB�ϵ�һ���㣬����DP��
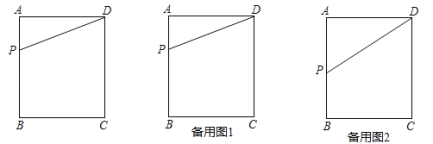
��1��������DAP��DP�۵�����A���ھ��εĶԽ����ϵ�A�䴦������AP�ij���
��2����P�˶���ijһʱ�̣�����P��ֱ��PE��BC�ڵ�E������DAP���PBE�ֱ���DP��PE�۵�����A���B�ֱ����ڵ�A�䣬B�䴦����P��A�䣬B������ǡ����ͬһֱ���ϣ���A��B�䣽2�������ʱAP�ij���
��3������P�˶�����AB���е㴦ʱ������P��ֱ��PG��BC�ڵ�G������DAP���PBG�ֱ���DP��PG�۵�����A���B�غ��ڵ�F��������CF�������CF�ij���
���𰸡���1��AP�ij�Ϊ![]() ��
��![]() ����2��PA�ij�Ϊ1��3����3��CF��
����2��PA�ij�Ϊ1��3����3��CF��![]() ��
��
��������
��1�����������Σ��ٵ���A���ڶԽ���BD��ʱ����AP=PA��=x���������̼��ɽ�����⣻�ڵ���A���ڶԽ���AC��ʱ���������������ε����ʹ������̼��ɽ�����⣻
��2�����������ηֱ���⼴�ɽ�����⣻
��3����ͼ5�У���FH��CD��H����취���FH��CH���ɽ�����⣻
��1��������A���ڶԽ���BD��ʱ����AP��PA����x��
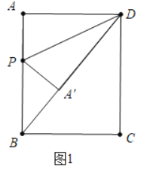
��Rt��ADB����AB��4��AD��3����BD��![]() ��5��
��5��
��AB��DA����3����BA����2��
��Rt��BPA������4��x��2��x2+22�����x��![]() ��
��
��AP��![]() ��
��
������A���ڶԽ���AC��ʱ��
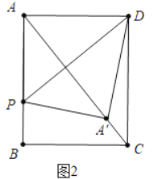
�ɷ������ʿ�֪��PD��AC��������DAP�ס�ABC��
��![]() ��
��![]() ����AP��
����AP��![]() ��
��![]() ��
��![]() ��
��
��AP�ij�Ϊ![]() ��
��![]() ��
��
��2������ͼ3�У���AP��x����PB��4��x��
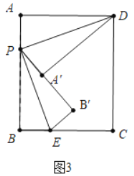
�����۵������ʿ�֪��PA��PA����x��PB��PB����4��x��
��A��B����2����4��x��x��2����x��1����PA��1��
����ͼ4�У�

��AP��x����PB��4��x��
�����۵������ʿ�֪��PA��PA����x��PB��PB����4��x��
��A��B����2����x����4��x����2��
��x��3����PA��3��
����������PA�ij�Ϊ1��3��
��3����ͼ5�У���FH��CD��H��
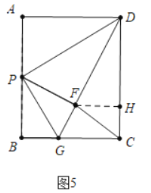
�ɷ��۵����ʿ�֪��AD��DF��3��BG��BF��G��F��D���ߣ�
��BG��FG��x����Rt��GCD����x+3��2��42+��3��x��2��
���x��![]() ����DG��DF+FG��
����DG��DF+FG��![]() ��CG��BC��BG��
��CG��BC��BG��![]() ��
��
��FH��CG����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��
��FH��![]() ��DH��
��DH��![]() ����CH��4��
����CH��4��![]() ��
��![]() ��
��
��Rt��CFH��CF��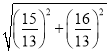 ��
��![]() ��
��

 Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д� ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�