题目内容
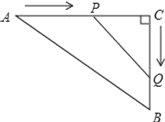
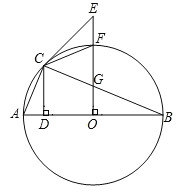
【题目】如图,△ACB内接于圆O,AB为直径,CD⊥AB与点D,E为圆外一点,EO⊥AB,与BC交于点G,与圆O交于点F,连接EC,且EG=EC.
(1)求证:EC是圆O的切线;
(2)当∠ABC=22.5°时,连接CF.
①求证:AC=CF;
②若AD=1,求线段FG的长.
【答案】(1)证明见解析;(2)①证明见解析;②2.
【解析】
(1)连接OC,证得OC⊥CE,即可证得结论;
(2)①通过证得∠AOC=45°=∠COF=45°,得出弧AC=弧CF,即可证得AC=CF;
②作CM⊥OE于M,首先证得CF=CG,得出CM垂直平分FG,然后通过三角形平分线的性质证得CM=CD,即可证得Rt△ACD≌Rt△FCM,从而证得FM=AD=1,即可证得FG=2FM=2.
(1)证明:连接OC,
∵OC=OB,
∴∠OCB=∠B,
∵EO⊥AB,
∴∠OGB+∠B=90°,
∵EG=EC,
∴∠ECG=∠EGC,
∵∠EGC=∠OGB,
∴∠OCB+∠ECG=∠B+∠OGB=90°,
∴OC⊥CE,
∴EC是圆O的切线;
(2)①证明:∵∠ABC=22.5°,∠OCB=∠B,
∴∠AOC=45°,
∵EO⊥AB,
∴∠COF=45°,
∴弧AC=弧CF,
∴AC=CF;
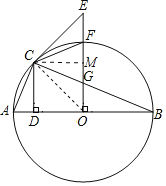
②解:作CM⊥OE于M,

∵AB为直径,
∴∠ACB=90°
∵∠ABC=22.5°,∠GOB=90°,
∴∠A=∠OGB=∠67.5°,
∴∠FGC=67.5°,
∵∠COF=45°,OC=OF,
∴∠OFC=∠OCF=67.5°,
∴∠GFC=∠FGC,
∴CF=CG,
∴FM=GM,
∵∠AOC=∠COF,CD⊥OA,CM⊥OF,
∴CD=DM,
在Rt△ACD和Rt△FCM中
![]()
∴Rt△ACD≌Rt△FCM(HL),
∴FM=AD=1,
∴FG=2FM=2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目