题目内容
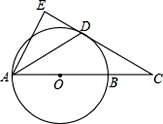
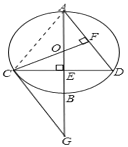
【题目】已知圆0的直径AB垂直于弦CD于点E,CG是圆O的切线交AB的延长线于点G,连接CO并延长交AD于点F,且CF![]() AD.
AD.
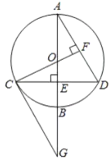
(1)试问:CG//AD吗?说明理由:
(2)证明:点E为OB的中点.
【答案】(1)平行,理由见解析(2)见解析.
【解析】
(1)根据切线的性质知CG⊥CF,再由已知条件CF⊥AD,可以根据在同一平面内,同时垂直于同一条直线的两条直线互相平行判定CG∥AD;
(2)连接AC构建等边三角形ACD,然后根据等边三角形的“三线合一”、三个内角都是60°的性质推知∠FCD=30°;最后利用垂径定理和30°的直角边是斜边的一半求得OE=![]() OB,即点E为OB的中点.
OB,即点E为OB的中点.
(1)CG∥AD,理由如下:
∵CG是⊙O的切线,OC是⊙O的半径,
∴CG⊥CF;
又∵CF⊥AD,
∴CG∥AD;
(2)如图(1),连接AC,
∵CF⊥AD,AE⊥CD,
且CF、AE过圆心O,![]()
∴AC=AD=CD,
∴△ACD是等边三角形,
∴∠D=60°,
∴∠FCD=30°;
在Rt△COE中,OE=![]() OC,
OC,
∴OE=![]() OB,
OB,
∴点E为OB的中点.

练习册系列答案
相关题目