题目内容
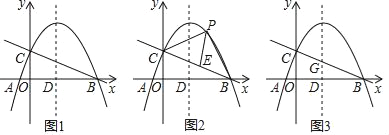
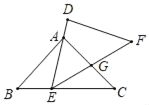
【题目】如图,在△ABC中,已知,AB=AC=6,BC=10.E是C边上一动点(E不与点B、C重合),△DEF≌△ABC.其中点A,B的对应点分别是点D、E,且点E在运动时,DE边始终经过点A,设EF与AC相交于点G,当△AEG为等腰三角形时,则BE的长为_____.
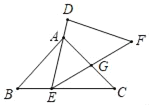
【答案】4或6.4.
【解析】
题目要求△AEG为等腰三角形,但没有说明哪两边为腰,这种一般都要分情况讨论,根据![]() ,且
,且![]() 为
为![]() 的外角,可得
的外角,可得![]() ,所以
,所以![]() ,首先排除一种情况,剩下两种
,首先排除一种情况,剩下两种![]() 与
与![]() ,根据全等三角形与相似三角形的性质求解即可.
,根据全等三角形与相似三角形的性质求解即可.
解:∵∠AEF=∠B=∠C,且∠AGE>∠C,
∴∠AGE>∠AEF,
∴AE≠AG;
当AE=EG时,则△ABE≌△ECG,
∴CE=AB=6,
∴BE=BC﹣EC=10﹣6=4;
当AG=EG时,则∠GAE=∠GEA,
∴∠GAE+∠BAE=∠GEA+∠CEG,
即∠CAB=∠CEA,
又∵∠C=∠C,
∴△CAE∽△CBA,
∴![]() =
=![]() ,
,
∴CE=![]() =
=![]() =3.6,
=3.6,
∴BE=10﹣3.6=6.4;
∴BE=4或6.4.
故答案为4或6.4.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目