��Ŀ����
����Ŀ����֪������![]() ����A��0��-3����B��-1��0�����������߶Գ���Ϊֱ��
����A��0��-3����B��-1��0�����������߶Գ���Ϊֱ��![]() ��E
��E
�������ߵĶ��㡣
(1)�������ߵĽ���ʽ�Լ���������E��
(2)��![]() �����Ƿ���ڵ�P��ʹ��
�����Ƿ���ڵ�P��ʹ��![]() �ܳ���̣������ڣ������P�����꣬�������ڣ���˵
�ܳ���̣������ڣ������P�����꣬�������ڣ���˵
�����ɡ�
(3)ֱ��![]() �������߽���C��D���㣬Q��ֱ��DC�·��������ϵ�һ�㣬�Ƿ���ڵ�Q
�������߽���C��D���㣬Q��ֱ��DC�·��������ϵ�һ�㣬�Ƿ���ڵ�Q
ʹ��![]() ����������������������������������ڣ���˵�����ɡ�
����������������������������������ڣ���˵�����ɡ�
(4)���������Ƿ���ڵ�M��ʹ��![]() ��ֱ�������Σ������ڣ�ֱ��д��M�����꣬����
��ֱ�������Σ������ڣ�ֱ��д��M�����꣬����
���ڣ���˵�����ɡ�
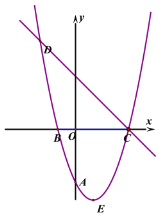
���𰸡�(1)y=(x-1)-4,E(1,-4);(2)������;(3)������;(4)������.
��������(1)��B,C����ֱ��![]() �Գƣ��ɵ�C�����ꣻ�ô���ϵ�����������ʽ��
�Գƣ��ɵ�C�����ꣻ�ô���ϵ�����������ʽ��
�������ꣻ
��2����A�����x��ĶԳƵ�F��0��3��������EF��x����P�㣬��ʱPA+PE��̣�
��3����Q����QH![]() �ᣬ��DC��K�㣬��Q
�ᣬ��DC��K�㣬��Q![]() ��K
��K![]() ��
��![]() ����QK�����ֵʱ��QDC��������ֵ��
����QK�����ֵʱ��QDC��������ֵ��
��4�����ڣ��Ȼ���ֱ���������ټ��㼴��.

��2����A�����x��ĶԳƵ�F��0��3��������EF��x����P�㣬��ʱPA+PE��̣�����ΪAE�ij��Ƕ�ֲ�����Դ�ʱ������PAE�ܳ���̣���ֱ��EFΪy=kx+b,�����֪��![]()
��3�������֪��D��-2��5��
��Q����QH![]() �ᣬ��DC��K�㣬��Q
�ᣬ��DC��K�㣬��Q![]() ��K
��K![]()
![]()
��QK�����ֵʱ��QDC��������ֵ.
QK=![]() ��
��
![]() ��0��
��0��![]()
���ԡ�QDC��������ֵΪ![]() ��
��
��4��![]() .
.