题目内容
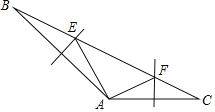
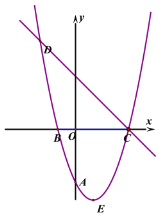
【题目】已知:如图,△ABC与△ADE,AB=AC,AD=AE,且∠BAC=∠DAE=40°,CD与BE相交于点F,连接AF则下列结论:①CD=BE:②△ABF≌△ACF;③∠BFD=140°;④FA平分∠BFD;⑤∠FAC=∠FAE.其中正确的结论有( )

A.2个B.3个C.4个D.5个
【答案】A
【解析】
根据已知条件易证△ABE≌△ACD,得到BE=CD即可判断①,根据两条边相等无法判断△ABF≌△ACF,根据已知条件不能得到∠BFC=40°,故可判断③,作AM⊥BE,AN⊥CD,根据全等三角形的性质得到AM=AN,可得AF平分∠BFD,故可判断④⑤.
∵∠BAC=∠DAE=40°,
∴∠BAC+∠CAE=∠DAE+∠CAE,
∴∠BAE=∠CAD,又AB=AC,AD=AE
∴△ABE≌△ACD
∴BE=CD,①正确;
∵AB=AC,AF=FA,∠BAF≠∠CAF,
∴△ABF与△ACF不全等,故②错误;
∴∠BAC≠∠BFC=40°,则∠BFD≠140°,③错误;
作AM⊥BE,AN⊥CD,∵△ABE≌△ACD
∴AM=AN,
∴AF平分∠BFD,AF不平分∠CAE,故④正确,⑤错误,
故选A.


 阅读快车系列答案
阅读快车系列答案【题目】 某校七年级共有男生63名,为了参加全校运动会,七年级准备从本年级所有男生中挑选出身高相差不多的40名男生组成仪仗队,为此,收集到所有男生的身高数据(单位:cm),经过整理获得如下信息:
a.小明把所有男生的身高数据按由低到高整理为如下,但因为不小心有部分数据被墨迹遮挡:

b.小刚绘制了七年级所有男生身高的频数分布表
身高分组 | 划记 | 频数 |
149≤x<152 | 丅 | 2 |
152≤x<155 | 正一 | 6 |
155≤x<158 | 正正丅 | 12 |
158≤x<161 | 正正正 | 19 |
161≤x<164 | 正正 | 10 |
164≤x<167 | ______ | ______ |
167≤x<170 | ______ | ______ |
170≤x<173 | 丅 | 2 |
c.该校七年级男生身高的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 |
160 | m | n |
根据以上信息,回答下列问题:
(1)补全b表中频数分布表;
(2)直接写出c表中m,n的值;
(3)借助于已给信息,确定挑选出参加仪仗队的男生的身高范围;
(4)若本区七年级共有男生1260名,利用以上数据估计,全区七年级男生身高达到160及以上的男生约有多少人?