题目内容
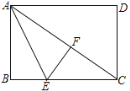
【题目】如图，已知矩形ABCD中，将△ABE沿着AE折叠至△AEF的位置，点F在对角线AC上．若BE＝3，EC＝5，则AB的长为_____.
【答案】6.
【解析】
根据折叠的性质得出AF=AB，EF=BE=3，在Rt△EFC中根据勾股定理求出CF=4，设AF=AB=x，则AC=x+4，在Rt△ABC中根据勾股定理列方程即可求出AB的长．
由△ABE沿着AE折叠至△AEF的位置可得：AF=AB，EF=BE=3，∠AFE=∠B=90°，
在Rt△EFC中根据勾股定理得CF=
=4，
设AF=AB=x，则AC=x+4，
在Rt△ABC中根据勾股定理得：AB2+BC2=AC2，
即x2+(3+5)2=(x+4)2，
解得：x=6，
即AB=6．
练习册系列答案
金钥匙试卷系列答案
相关题目
【题目】某市为了鼓励居民节约用水，采用分阶段计费的方法按月计算每户家庭的水费：月用水量不超过20m3时，按2元/m3计算；月用水量超过20m3时，其中的20m3仍按2元/m3计算，超过部分按2.6元/m3计算．设某户家庭月用水量xm3．
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
（1）用含x的式子表示：
当0≤x≤20时，水费为 元；
当x＞20时，水费为 元．
（2）小花家第二季度用水情况如上表，小花家这个季度共缴纳水费多少元？
