题目内容
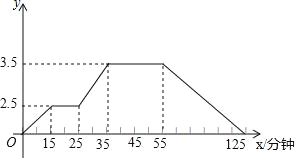
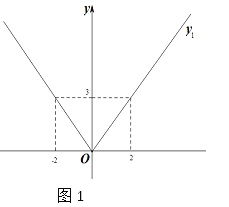
【题目】(1)写出图1中函数图象的解析式y1=_________________.
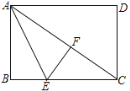
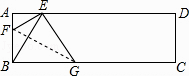
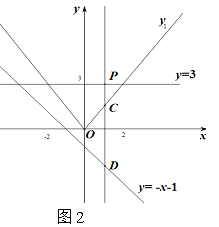
(2)如图2,过直线y=3上一点P(m,3)作x轴的垂线交y1的图象于点C,交y= -x- 1于点D.
①当m>0时,试比较PC与PD的大小,并证明你的结论.
②若CD<3时,求m的取值范围.
【答案】(1)y1=![]() 或y1=
或y1=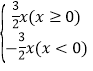 (2)①当0<m<14时,PC<PD;当m=14时,PC=PD;当m>14时,PC>PD;②-4<m<
(2)①当0<m<14时,PC<PD;当m=14时,PC=PD;当m>14时,PC>PD;②-4<m<![]()
【解析】
(1)设函数的解析式为y=kx,
当x≥0时,把(2,3)代入解析式求出k的值,
当x<0时,把(-2,3)代入解析式求出k的值,
综合以上两种情况即可得出函数的解析式;
(2)①结合图象,分0<m≤2、2<m<14、m=14、m>14四种情况进行讨论即可得出结论;
②分m≥0和m<0两种情况列出不等式进行解答即可.
(1)y1=![]() 或y1=
或y1=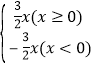 ;
;
(2)①A.当0<m≤2时,显然PC<PD;
B.当m>2时,
PC=![]() m-3,PD=m+4,
m-3,PD=m+4,
令![]() m-3=m+4,
m-3=m+4,
∴m=14,
∴当2<m<14时,PC<PD;当吗m=14时,PC=PD;当m>14时,PC>PD.
∴综上可知:当0<m<14时,PC<PD;
当m=14时,PC=PD;
当m>14时,PC>PD;
②A.当m≥0时,
CD=![]() m-(-m-1)=
m-(-m-1)=![]() m +1,
m +1,
∴![]() m+1<3,
m+1<3,
∴0≤m<![]() ;
;
B.当m<0时,
CD=-![]() m-(-m-1)= -
m-(-m-1)= -![]() m+1,
m+1,
∴-![]() m+1<3,
m+1<3,
∴-4<m<0;
∴综上可知:-4<m<![]() .
.

【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,
组别 | 课堂发言次数n |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
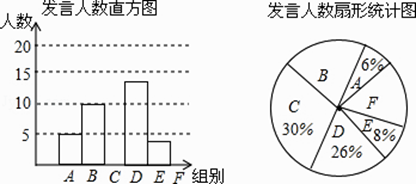
请结合图中相关数据回答下列问题:
(1)样本容量是 , 并补全直方图;
(2)该年级共有学生800人,请估计该年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰好有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好都是男生的概率.