题目内容
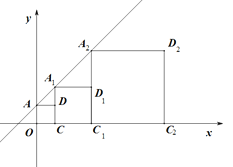
【题目】如图，正方形AOCD、正方形A1CC1D1、正方形A2C1C2D2的顶点A、A1、A2和O、C、C1、C2分别在一次函数y＝x+1的图象和x轴上，若正比例函数y＝kx则过点D5，则系数k的值是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
先根据点A是直线y=x+1与y轴的交点求出点A的坐标，然后根据正方形的性质求出点D的坐标，将点D的横坐标代入y=x+1求出点A1的纵坐标，进而得出点A1的坐标，同理得出点D1、A2、D2、A3、D3的坐标，找出规律，得出D5的坐标，然后把D5的坐标代入y=kx中即可求出k的值．
∵点A是直线y=x+1与y轴的交点，
∴A（0，1），
∵四边形AOCD是正方形，
∴D（1，1），
∵点A1在直线y=x+1上，
∴A1（1，2），
同理可得D1（3，2），A2（3，4），D2（7，4），A3（7，8），D3（15，8），……
∴D1（3，2），D2（7，4），D3（15，8），……
∴Dn的坐标是（2n+1-1，2n）．
∴D5（63，32），
把D5（63，32）代入y=kx得：k=
．
故选：B．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
