题目内容
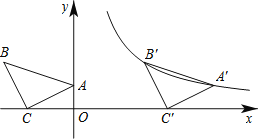
【题目】如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,![]() 是
是![]() 的外角
的外角![]() 的角平分线,延长
的角平分线,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
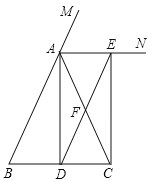
(1)求证:四边形![]() 是矩形;
是矩形;
(2)填空:
①若![]() ,则四边形
,则四边形![]() 的面积为_______;
的面积为_______;
②当![]() 满足______时,四边形
满足______时,四边形![]() 是正方形.
是正方形.
【答案】(1)见解析;(2)①![]() ;②答案不唯一,如当
;②答案不唯一,如当![]() 时,或者,当
时,或者,当![]() 时,
时,
【解析】
(1)根据AN是△ABC外角∠CAM的平分线,推得∠MAE=![]() (∠B+∠ACB),再由∠B=∠ACB,得∠MAE=∠B,则AN∥BC,根据CE⊥AN,得出四边形ADCE为矩形.
(∠B+∠ACB),再由∠B=∠ACB,得∠MAE=∠B,则AN∥BC,根据CE⊥AN,得出四边形ADCE为矩形.
(2)①先证明四边形ABDE为平行四边形,由条件可证明△ABC为等边三角形,求出BD和AD长,则四边形ABDE的面积可求出;
②由(1)知四边形ADCE是矩形,增加条件能使AD=DC即可.
(1)∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=![]() ∠MAC,
∠MAC,
∵∠MAC=∠B+∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠MAE=∠B,
∴AN∥BC,
∵AB=AC,点D为BC中点,
∴AD⊥BC,
∵![]() ,
,![]() 是
是![]() 中点,
中点, ![]() 是
是![]() 的外角
的外角![]() 的角平分线,
的角平分线,
∴AD平分∠BAC, ![]() 是
是![]() 的外角
的外角![]() 的角平分线,
的角平分线,
∴CE⊥AN,
∵CE⊥AN,
∴AD∥CE,
∴四边形ADCE为平行四边形,
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形;
(2)①解:∵AB=AC,D是BC中点,F是AC中点,
∴DF∥AB,
由(1)知AE∥BD,
∴四边形ABDE是平行四边形,
∵BC=AB=4,AB=AC,
∴△ABC是等边三角形,
∴∠ABD=60°,
∵D为BC的中点,
∴∠ADC=90°,BD=2,
∴AD=BDtan60°=2×![]() =2
=2![]() ,
,![]() =4
=4![]() ,
,
故答案为:4![]() ;
;
②解:答案不唯一,如当∠BAC=90°时,四边形ADCE是正方形.
∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,
∵D为BC的中点,
∴AD=DC,
∵四边形ADCE为矩形,
∴四边形ADCE为正方形.
故答案为:∠BAC=90°.