题目内容
【题目】在半径为2的⊙O中，弦AB=
，连接OA,OB.在直线OB上取一点K，使tan∠BAK=
，则ΔOAK的面积为___________.
【答案】
或6
【解析】
根据题意，建立直角三角形，根据锐角三角函数值求得OK的长度，从而求得三角形面积.
解：
情况一：如图，过点K作KM⊥AB
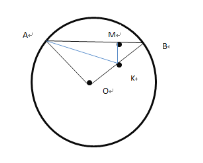
由题意可知，OA=OB=2,AB=
∵
∴△AOB为等腰直角三角形
∴∠OAB=∠OBA=45°
∵tan∠BAK=
∴在Rt△AKM中，
设MK=x,则AM=2x,MB=x,则AB=3x
∴3x=
解得：x=
∴MK=MB=，BK=
∴OK=OB-BK=
∴S△AOK=
情况二：如图，过点K作KM⊥AB
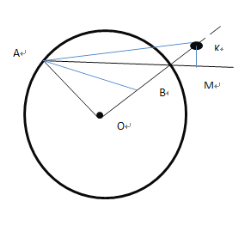
由题意可知，OA=OB=2,AB=
∵
∴△AOB为等腰直角三角形
∴∠OAB=∠OBA=45°
∵tan∠BAK=
∴在Rt△AKM中，
设MK=x,则AM=2x,MB=x,则AB=x
∴x=
∴BK=
∴OK=OB-BK=
∴S△AOK=
综上所述，故答案为：或6
练习册系列答案
相关题目
