题目内容
【题目】如图，正方形ABCO的顶点A、C分别在y轴、x轴上，以AB为弦的⊙M与x轴相切.若点A的坐标为（0，8），则圆心M的坐标为__________.
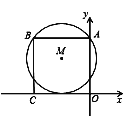
【答案】(-4,5)
【解析】
设切点为D，连接DM并延长交AB于E，连接BM，先证△BME是直角三角形，再利用勾股定理列方程即可.
解：设切点为D，连接DM并延长交AB于E，连接BM，设圆的半径为r
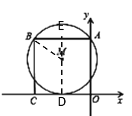
∵⊙M与x轴相切
∴MD⊥CO
又∵四边形ABCO为正方形
∴DE⊥AB，四边形BCDE和四边形EDOA为矩形
∵点A的坐标为（0，8）
∴且AB=DE=BC=CO=OA=8
∵DE过⊙M的圆心
∴BE=AE=
BA=4
∵BM=r，ME=8－r
在Rt△BME中
r2－（8－r）2=42
解得：r=5
∴MD=5，OD=AE=4，
∵M在第二象限
∴M的坐标为：(-4,5)
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
