题目内容
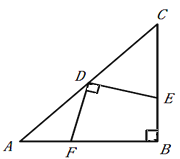
【题目】如图,矩形ABCD绕点C顺时针旋转90°后得到矩形CEFG,连接DG交EF于H,连接AF交DG于M;
(1)求证:AM=FM;
(2)若∠AMD=a.求证:![]() =cosα.
=cosα.

【答案】(1)见解析;(2)见解析.
【解析】
(1)由旋转性质可知:AD=FG,DC=CG,可得∠CGD=45°,可求∠FGH=∠FHG=45°,则HF=FG=AD,所以可证△ADM≌△MHF,结论可得.
(2)作FN⊥DG垂足为N,且MF=FG,可得HN=GN,且DM=MH,可证2MN=DG,由第一问可得2MF=AF,由cosα=cos∠FMG=![]() ,代入可证结论成立
,代入可证结论成立
(1)由旋转性质可知:
CD=CG且∠DCG=90°,
∴∠DGC=45°从而∠DGF=45°,
∵∠EFG=90°,
∴HF=FG=AD
又由旋转可知,AD∥EF,
∴∠DAM=∠HFM,
又∵∠DMA=∠HMF,
∴△ADM≌△FHM
∴AM=FM
(2)作FN⊥DG垂足为N
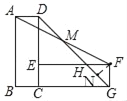
∵△ADM≌△MFH
∴DM=MH,AM=MF=![]() AF
AF
∵FH=FG,FN⊥HG
∴HN=NG
∵DG=DM+HM+HN+NG=2(MH+HN)
∴MN=![]() DG
DG
∵cos∠FMG=![]()
∴cos∠AMD=![]()
∴![]() =cosα
=cosα

练习册系列答案
相关题目